Bài 10 trang 79 Toán 10 Tập 1 Chân trời sáng tạo

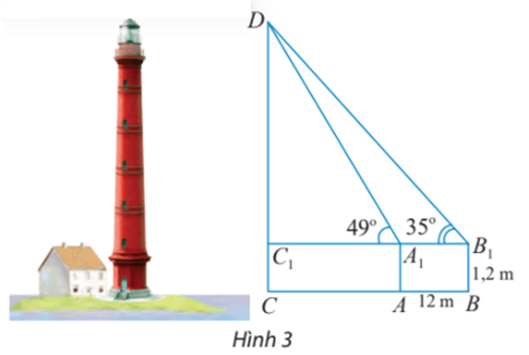
Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2 m. Gọi D là đỉnh tháp và hai điểm A, B cùng thẳng hàng với C thuộc chiều cao CD của tháp. Người ta đo được . Tính chiều cao CD của tháp.

Giải Toán lớp 10 Bài tập cuối chương 4

Bài 10 trang 79 Toán lớp 10 Tập 1: Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2 m. Gọi D là đỉnh tháp và hai điểm A₁, B₁ cùng thẳng hàng với C₁ thuộc chiều cao CD của tháp. Người ta đo được $\widehat{D{A}_1{C}_1}={49}^o,\widehat{D{B}_1{C}_1}={35}^o$. Tính chiều cao CD của tháp.

Lời giải:

Do phương nằm ngang hợp với phương thẳng đứng của tháp góc 90° nên hai tam giác DC₁A₁ và DC₁B₁ là hai tam giác vuông tại C₁.

Tam giác DC₁A₁ có : tan49° = $\frac{D{C}_1}{C_1{A}_1}$  ⇒ DC₁ = C₁A₁tan49°        (1).

Tam giác DC₁B₁ có : tan35° = $\frac{D{C}_1}{C_1{B}_1}=\frac{D{C}_1}{C_1{A}_1+A_1{B}_1}=\frac{D{C}_1}{C_1{A}_1+12}$ 

⇒ DC₁ = (C₁A₁ + 12). tan35° = C₁A₁ tan35° + 12tan35°             (2).

Từ (1) và (2) suy ra: C₁A₁tan49° = C₁A₁ tan35° + 12tan35°

⇒ C₁A₁ = $\frac{12\tan {35}^o}{\tan {49}^o-\tan {35}^o}$ ≈ 18,7.

⇒ DC₁ = C₁A₁tan49° ≈ 18,7.tan49° ≈ 21,5.

Mà DC = DC₁ + C₁C  = 21,5 + 1,2 = 22,7.

Vậy chiều cao của tháp CD khoảng 22,7 m.

Lời giải bài tập Toán 10 Bài tập cuối chương 4 hay, chi tiết khác:

• Bài 1 trang 78 Toán lớp 10 Tập 1: Cho tam giác ABC. Biết a = 49,4; b = 26,4, $\widehat{C}={47}^{o}20\text{'}$. Tính hai góc $\widehat{A};\widehat{B}$ và cạnh c ....

• Bài 2 trang 78 Toán lớp 10 Tập 1: Cho tam giác ABC. Biết a = 24, b = 13, c = 15. Tính các góc $\widehat{A}\text{, }\widehat{B}\text{, }\widehat{C}$ ....

• Bài 3 trang 78 Toán lớp 10 Tập 1: Cho tam giác ABC có a = 8, b = 10, c = 13. Tam giác ABC có góc tù không? ....

• Bài 4 trang 79 Toán lớp 10 Tập 1: Cho tam giác ABC có $\widehat{A}={120}^o$ , b = 8, c = 5. Tính Cạnh a và các góc $\widehat{B}, \widehat{C}$ ....

• Bài 5 trang 79 Toán lớp 10 Tập 1: Cho hình bình hành ABCD. Chứng minh 2(AB² + BC²) = AC² + BD² ....

• Bài 6 trang 79 Toán lớp 10 Tập 1: Cho tam giác ABC có a = 15, b = 20, c = 25. Tính diện tích tam giác ABC ....

• Bài 7 trang 79 Toán lớp 10 Tập 1: Cho tam giác ABC. Chứng minh rằng cotA + cotB + cotC = $\frac{R(a^2+b^2+c^2)}{abc}$ ....

• Bài 8 trang 79 Toán lớp 10 Tập 1: Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ tinh đến A và B là 2,1° ....

• Bài 9 trang 79 Toán lớp 10 Tập 1: Hai chiếc tàu thủy P và Q cách nhau 300 m và thẳng hàng với chân B ....