Cho hàm số f( x ) = - 1/x - 1; khi x nhỏ hơn hoặc bằng 0; căn bậc hai của (x + 2) ,khi x > 0. Tập xác định của hàm số là tập hợp nào sau đây? A. [–2; +∞); B. ℝ; C. ℝ
Câu hỏi:
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{ - 1}}{{x - 1}},\,\,\,\,\,\,\,\,khi\,\,x \le 0\\\sqrt {x + 2} ,\,\,\,khi\,\,x > 0\end{array} \right.\). Tập xác định của hàm số là tập hợp nào sau đây?
A. [–2; +∞);
B. ℝ;
C. ℝ \ {1};
D. {x ∈ ℝ | x ≠ 1 và x ≠ –2}.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
Trường hợp 1: x ≤ 0.
Biểu thức f(x) = \(\frac{{ - 1}}{{x - 1}}\) xác định khi và chỉ khi x – 1 ≠ 0.
Nghĩa là, x ≠ 1.
Giao với điều kiện x ≤ 0, ta được x ≤ 0.
Trường hợp 2: x > 0.
Biểu thức f(x) = \(\sqrt {x + 2} \) xác định khi và chỉ khi x + 2 ≥ 0.
Nghĩa là, x ≥ –2.
Giao với điều kiện x > 0, ta được x > 0.
Vì vậy khi hợp điều kiện của trường hợp 1 và trường hợp 2, ta thu được tập xác định của hàm số là D = ℝ.
Vậy ta chọn phương án B.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Cho hai đại lượng x và y phụ thuộc vào nhau theo các hệ thức dưới đây. Trường hợp nào thì y không phải là hàm số của x?
Xem lời giải »
Câu 2:
Tập xác định D của hàm số \[f\left( x \right) = 2\sqrt {x + 1} - \frac{5}{x}\].
Xem lời giải »
Câu 4:
Xét sự đồng biến, nghịch biến của hàm số \[f\left( x \right) = \frac{3}{x}\] trên khoảng (0; +∞). Khẳng định nào sau đây đúng?
Xem lời giải »
Câu 5:
Hàm số y = f(x) có đồ thị như hình vẽ bên.
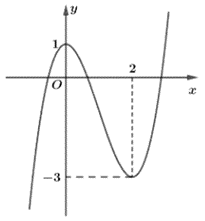
Khẳng định nào sau đây đúng?
Xem lời giải »
Câu 6:
Xét tính đồng biến, nghịch biến của hàm số \(y = \sqrt[3]{x} + 3\).
Xem lời giải »


