Cho hình vuông ABCD tâm O cạnh a. Gọi M là trung điểm AB, N là điểm đối xứng

Câu hỏi:

A. $\left|\overrightarrow{MN}\right|=\frac{a\sqrt{15}}{2}$

B. $\left|\overrightarrow{MN}\right|=\frac{a\sqrt{5}}{3}$

C. $\left|\overrightarrow{MN}\right|=\frac{a\sqrt{13}}{2}$

D. $\left|\overrightarrow{MN}\right|=\frac{a\sqrt{5}}{4}$

Trả lời:

Hướng dẫn giải

Đáp án đúng là: C

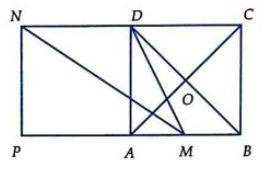
Vì M là trung điểm AB nên ta có AM = $\frac{AB}{2}=\frac{a}{2}$.

Tam giác MAD vuông tại A: $D{M}^2=A{M}^2+A{D}^2$ (Định lý Pytago)

$\iff D{M}^2={\left(\frac{a}{2}\right)}^2+a^2=\frac{5a^2}{4}$

$\Rightarrow DM=\frac{a\sqrt{5}}{2}$.

Qua N kẻ đường thẳng song song với AD cắt AB tại P.

Ta có NP // AD, mà AD ⊥ CN (vì ABCD là hình vuông)

Do đó NP ⊥ CN hay NP ⊥ ND.

Suy ra $\widehat{PND}=90°$  (1).

Vì AD ⊥ ND nên $\widehat{ADN}=90°$  (2).

Tương tự, AD ⊥ AP nên $\widehat{PAD}=90°$ (3).

Từ (1) (2) (3), ta suy ra tứ giác ADNP là hình chữ nhật (4).

Vì N là điểm đối xứng của C qua D nên ND = CD = a.

Mà AD = a (do ABCD là hình vuông cạnh a).

Nên ND = AD = a (5).