Giải Toán 10 trang 40 Tập 2 Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm giải Toán 10 trang 40 Tập 2 trong Bài 1: Toạ độ của vectơ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 40.
Giải Toán 10 trang 40 Tập 2 Chân trời sáng tạo
Thực hành 1 trang 40 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho ba điểm D(-1; 4), E(0; -3), F(5; 0).
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy.
b) Tìm tọa độ của các vectơ .
c) Vẽ và tìm tọa độ hai vectơ đơn vị và lần lượt trên hai trục tọa độ Ox và Oy.
Lời giải:
a) Các điểm D, E, F được biểu diễn trên mặt phẳng Oxy như sau:
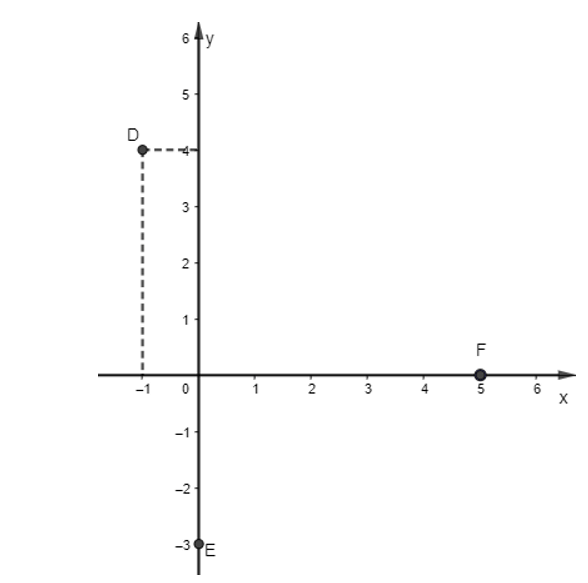
b) Tọa độ vectơ được gọi là tọa độ của điểm D nên .
Tọa độ vectơ được gọi là tọa độ của điểm E nên .
Tọa độ vectơ được gọi là tọa độ của điểm F nên .
c) Hai vectơ đơn vị và được biểu diễn lần lượt trên hai trục tọa độ Ox và Oy là:
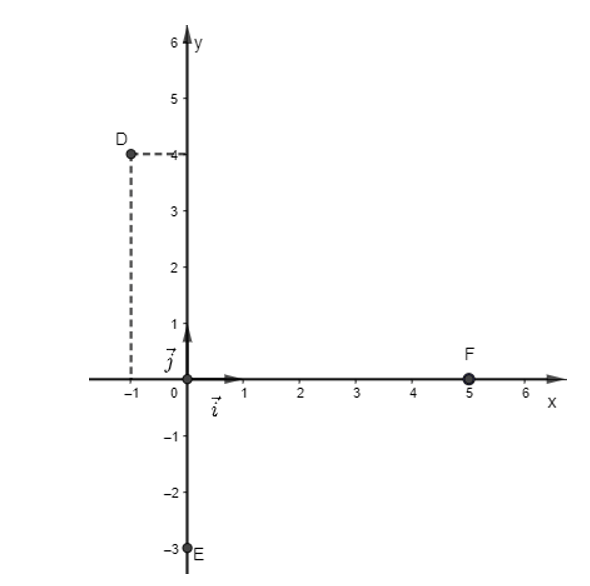
Tọa độ của vectơ và .
Vận dụng 1 trang 40 Toán lớp 10 Tập 2: Một máy bay đang cất cánh với vận tốc 240km/h theo phương hợp với phương nằm ngang một góc 30° (Hình 7).
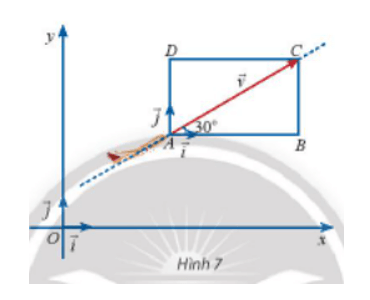
a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD.
b) Biểu diễn vectơ vận tốc theo hai vectơ và .
c) Tìm tọa độ vectơ của .
Lời giải:
a)
Xét tam giác ABC vuông tại B, có:
AB = cos30°.AC = 120
BC = sin30°.AC = 120
Vậy AB = DC = 120 và AD = BC = 120.
b) Vectơ cùng phương và cùng chiều với vectơ .
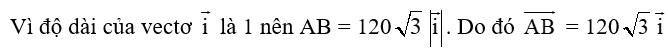
Vectơ cùng phương và cùng chiều với vectơ .
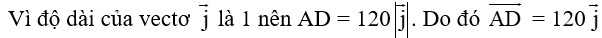
Xét hình chữ nhật ABCD, có:
(quy tắc hình bình hành)
⇒
⇒ .
c) Vì nên tọa độ của vectơ .
Hoạt động khám phá 4 trang 40 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai vectơ = (a1; a2), = (b1; b2) và số thực k. Ta đã biết có thể biểu diễn từng vectơ , theo hai vectơ , như sau: ; .
a) Biểu diễn từng vectơ , ; k theo hai vectơ , .
b) Tìm . theo tọa độ của hai vectơ , .
Lời giải:
a) Ta có:
;
;
.
b) Ta có:
. =
= a1b1 + a2b2 (vì và ).
Lời giải bài tập Toán lớp 10 Bài 1: Toạ độ của vectơ Chân trời sáng tạo hay khác: