Giải Toán 10 trang 44 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 44 Tập 2 trong Bài 1: Toạ độ của vectơ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 44.

Giải Toán 10 trang 44 Tập 2 Chân trời sáng tạo

Thực hành 5 trang 44 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho tam giác DEF có tọa độ đỉnh là D(2; 2), E(6; 2) và F(2; 6).

a) Tìm tọa độ điểm H là chân đường cao của tam giác DEF kẻ từ D.

b) Giải tam giác DEF.

Lời giải:

a) Gọi H(x_H; y_H).

Ta có: $\overrightarrow{DH}\left(x_H-2;y_H-2\right)$, $\overrightarrow{EF}\left(-4;4\right)$, $\overrightarrow{EH}\left(x_H-6;y_H-2\right)$

Vì H thuộc EF nên $\overrightarrow{EF}$ và $\overrightarrow{EH}$ cùng phương.

Khi đó: $\frac{x_H-6}{-4}=\frac{y_H-2}{4}\iff x_H=-y_H+8$

⇒ $\overrightarrow{DH}\left(-y_H+6;y_H-2\right)$

Vì DH $\perp$ EF nên $\overrightarrow{DH}.\overrightarrow{FE}=0$

⇔ (-y_H + 6).(-4) + (y_H – 2).4 = 0

⇔ 4y_H – 24 + 4y_H – 8 = 0

⇔ 8y_H = 32

⇔ y_H = 4

⇒ x_H = - 4 + 8 = 4

Vậy H(4; 4).

b) Ta có:

$\overrightarrow{DE}\left(6-2;2-2\right)=\left(4;0\right)$ ⇒ DE = $\sqrt{4^2+0^2}=4$;

$\overrightarrow{EF}\left(-4;4\right)$ ⇒ EF = $\sqrt{{\left(-4\right)}^2+4^2}=4\sqrt{2}$;

$\overrightarrow{DF}\left(2-2;6-2\right)=\left(0;4\right)$ ⇒ DF = $\sqrt{0^2+4^2}=4$;

Ta lại có EF² = ${\left(4\sqrt{2}\right)}^2$= 32 và DE² + DF² = 4² + 4² = 32

Suy ra EF² = DE² + DF²

Theo định lí Py – ta – go đảo ta có: ∆DEF vuông tại D

Mà DE = DF nên tam giác DEF vuông cân tại D.

Suy ra $\hat{D}=90°,\hat{E}=\hat{F}=45°$.

Vậy DE = DF = 4, EF = 4$\sqrt{2}$, $\hat{D}=90°,\hat{E}=\hat{F}=45°$.

Vận dụng 3 trang 44 Toán lớp 10 Tập 2: Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ B(50; 30) và C(32; -23). Một con tàu đang neo đậu tại điểm A(-10; 20).

a) Tính số đo của $\widehat{BAC}$.

b) Cho biết một đơn vị trên hệ trục tọa độ tương ứng với 1km. Tính khoảng cách từ con tàu đến mỗi hòn đảo.

Lời giải:

a) Ta có: $\overrightarrow{AB}\left(60;10\right)$ và $\overrightarrow{AC}\left(42;-43\right)$

Khi đó $\overrightarrow{AB}.\overrightarrow{AC}=$60.42 + 10.(-43) = 2 090

Ta lại có:

cos$\widehat{BAC}$

= cos$\left(\overrightarrow{AB};\overrightarrow{AC}\right)=\frac{\overrightarrow{AB}.\overrightarrow{AC}}{\left(\overrightarrow{AB}\right).\left(\overrightarrow{AC}\right)}=\frac{2090}{10\sqrt{37}.\sqrt{3613}}\approx 0.57$

⇒$\widehat{BAC}$ ≈ 55,24°.

Vậy $\widehat{BAC}$ ≈ 55,24°.

b) Ta có:

$\overrightarrow{AB}\left(60;10\right)$ ⇒ AB = $\sqrt{{60}^2+{10}^2}=10\sqrt{37}$≈ 60,83.

$\overrightarrow{AC}\left(42;-43\right)$ ⇒ AC = $\sqrt{{42}^2+{\left(-43\right)}^2}=\sqrt{3613}$≈ 60,11.

Vì một đơn vị trên hệ trục tọa độ tương ứng với 1km nên khoảng cách từ vị trí của con tàu tới đảo B là 60,83 km và tới đảo C là 60,11 km.

Bài 1 trang 44 Toán lớp 10 Tập 2: Trên trục (O; $\overrightarrow{e}$) cho các điểm A, B, C, D có tọa độ lần lượt là 4; -1; -5; 0.

a) Vẽ trục và biểu diễn các điểm đã cho trên trục đó.

b) Hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng hướng hay ngược hướng?

Lời giải:

a) Các điểm A, B, C, D được biểu diễn trên trục số là:

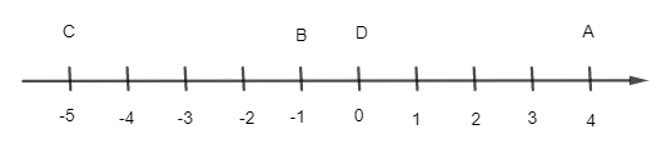
b) Quan sát hình vẽ ta thấy:

Hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ ngược hướng nhau.

Lời giải bài tập Toán lớp 10 Bài 1: Toạ độ của vectơ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 38 Tập 2

• Giải Toán 10 trang 39 Tập 2

• Giải Toán 10 trang 40 Tập 2

• Giải Toán 10 trang 41 Tập 2

• Giải Toán 10 trang 42 Tập 2

• Giải Toán 10 trang 43 Tập 2

• Giải Toán 10 trang 45 Tập 2