Bài 7.16 trang 47 Toán 10 Tập 2 - Kết nối tri thức
Trong mặt phẳng tọa độ, cho tam giác ABC, với A(6; – 2), B(4; 2), C(5; –5). Viết phương trình đường tròn ngoại tiếp tam giác đó.
Giải Toán lớp 10 Bài 21: Đường tròn trong mặt phẳng tọa độ
Bài 7.16 trang 47 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho tam giác ABC, với A(6; – 2), B(4; 2), C(5; –5). Viết phương trình đường tròn ngoại tiếp tam giác đó.
Lời giải:
Đường tròn ngoại tiếp tam giác ABC là đường tròn đi qua ba điểm A, B, C.
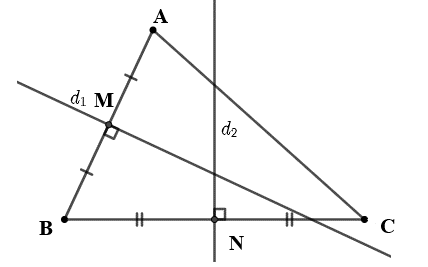
Các đoạn thẳng AB, BC tương ứng có trung điểm là M(5; 0), N.
Đường thẳng trung trực d1 của đoạn thẳng AB đi qua điểm M(5; 0) và có vectơ pháp tuyến .
Vì cùng phương với nên d1 cũng nhận là vectơ pháp tuyến. Do đó, phương trình của d1 là: 1(x – 5) – 2(y – 0) = 0 hay x – 2y – 5 = 0.
Đường thẳng trung trực d2 của đoạn thẳng BC đi qua N và có vectơ pháp tuyến , do đó phương trình d2 là: hay x – 7y – 15 = 0.
Tâm I của đường tròn (C) ngoại tiếp tam giác ABC cách đều ba điểm A, B, C nên I là giao điểm của d1 và d2.
Vậy tọa độ của I là nghiệm của hệ phương trình .
Suy ra I(1; – 2). Đường tròn (C) có bán kính là IA = .
Vậy phương trình của (C) là: (x – 1)2 + (y + 2)2 = 25.
Lời giải bài tập Toán 10 Bài 21: Đường tròn trong mặt phẳng tọa độ hay, chi tiết khác: