HĐ2 trang 46 Toán 10 Tập 2 - Kết nối tri thức
Cho đường tròn (C): (x – 1)+ (y – 2) = 25 và điểm M(4; – 2).
Giải Toán lớp 10 Bài 21: Đường tròn trong mặt phẳng tọa độ
HĐ2 trang 46 Toán 10 Tập 2: Cho đường tròn (C): (x – 1)2+ (y – 2)2 = 25 và điểm M(4; – 2).
a) Chứng minh điểm M(4; – 2) thuộc đường tròn (C).
b) Xác định tâm và bán kính của (C).
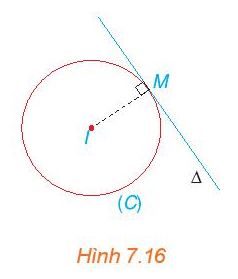
c) Gọi ∆ là tiếp tuyến của (C) tại M. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆ (H.7.16). Từ đó, viết phương trình đường thẳng ∆.
Lời giải:
a) Thay tọa độ điểm M(4; – 2) vào phương trình đường tròn (C) ta được:
(4 – 1)2 + (– 2 – 2)2 = 25 ⇔ 32 + (– 4)2 = 25 ⇔ 25 = 25 (luôn đúng).
Vậy điểm M(4; – 2) thuộc đường tròn (C).
b) Đường tròn (C) có tâm I(1; 2) và bán kính R = = 5.
c) Ta có: ∆ ⊥ IM tại M (bán kính đi qua tiếp điểm thì vuông góc với tiếp tuyến tại tiếp điểm đó).
Do đó một vectơ pháp tuyến của đường thẳng ∆ là vectơ .
Đường thẳng ∆ đi qua điểm M(4; – 2) và có một vectơ pháp tuyến nên phương trình đường thẳng ∆ là: 3(x – 4) – 4(y + 2) = 0 hay 3x – 4y – 20 = 0.
Lời giải bài tập Toán 10 Bài 21: Đường tròn trong mặt phẳng tọa độ hay, chi tiết khác: