Luyện tập 4 trang 39 Toán 10 Tập 2 - Kết nối tri thức

Cho đường thẳng ∆: y = ax + b với a ≠ 0.

Giải Toán lớp 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Luyện tập 4 trang 39 Toán 10 Tập 2: Cho đường thẳng ∆: y = ax + b với a ≠ 0.

a) Chứng minh rằng ∆ cắt trục hoành.

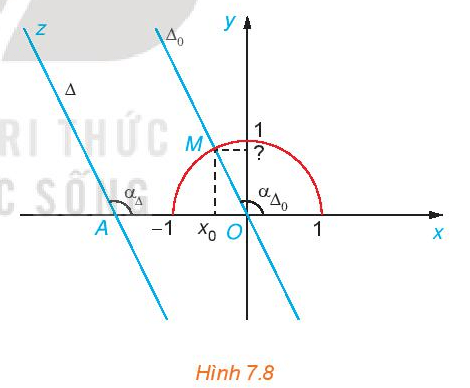
b) Lập phương trình đường thẳng ∆₀ đi qua O(0; 0) và song song (hoặc trùng) với ∆.

c) Hãy chỉ ra mối quan hệ giữa α_∆ và α_∆0.

d) Gọi M là giao điểm của ∆₀ với nửa đường tròn đơn vị và x₀ là hoành độ của M. Tính tung độ của M theo x₀ và a. Từ đó, chứng minh rằng tanα_∆ = a.

Luyện tập 4 trang 39 Toán 10 Tập 2 | Kết nối tri thức Giải Toán lớp 10

Lời giải:

a) Phương trình trục hoành Ox: y = 0.

Xét hệ $\{\begin{cases} y = 0 \\ y = a x + b \end{cases}$ .

Khi đó ta có: ax + b = 0 ⇔ x = $- \frac{b}{a}$ (do a ≠ 0).

Do đó hệ trên có nghiệm duy nhất $(- \frac{b}{a}; 0)$ nên ∆ và trục hoành cắt nhau tại giao điểm có tọa độ $(- \frac{b}{a}; 0)$ .

b) Đường thẳng ∆ có vectơ pháp tuyến là $\vec{n} = (a; - 1)$ .

Do đường thẳng ∆₀ song song hoặc trùng với ∆ nên ta chọn vectơ $\vec{n}$ là một vectơ pháp tuyến của ∆₀.

Đường thẳng ∆₀ đi qua điểm O(0; 0) và nhận $\vec{n} = (a; - 1)$ làm vectơ pháp tuyến.

Khi đó phương trình đường thẳng ∆₀ là: a(x – 0) – (y – 0) = 0 hay ax – y = 0 hay y = ax.

c) Khi ∆ và ∆₀ trùng nhau thì α_∆ và α_∆0 trùng nhau nên α_∆ = α_∆0.

Khi ∆ và ∆₀ song song thì α_∆ = α_∆0 (do hai góc ở vị trí đồng vị).

Vậy α_∆ = α_∆0.

d) Vì M thuộc đường thẳng ∆₀ nên tọa độ điểm M thỏa mãn phương trình đường thẳng ∆₀ nên khi có hoành độ x₀ thì tung độ của M là y₀ = ax₀.

Ta có tanα_∆0 = tan∠xOM = $\frac{y_{0}}{x_{0}} = \frac{a x_{0}}{x_{0}} = a$ (theo định nghĩa giá trị lượng giác)

Do α_∆ = α_∆0 nên tanα_∆ = tanα_∆0 = a.

Vậy tanα_∆ = a.

Lời giải bài tập Toán 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách hay, chi tiết khác:

<<<<<<< HEAD ======= >>>>>>> 7de0ce75c76253c52280308e94cf2d713ccea5e2