Vận dụng trang 41 Toán 10 Tập 2 - Kết nối tri thức

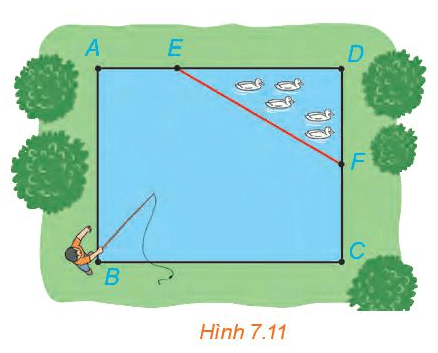
Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15 m, chiều rộng AB = 12 m. Phần tam giác DEF là nơi ông bà nuôi vịt, AE = 5 m, CF = 6 m (H.7.11).

Giải Toán lớp 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Vận dụng trang 41 Toán 10 Tập 2: Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15 m, chiều rộng AB = 12 m. Phần tam giác DEF là nơi ông bà nuôi vịt, AE = 5 m, CF = 6 m (H.7.11). 

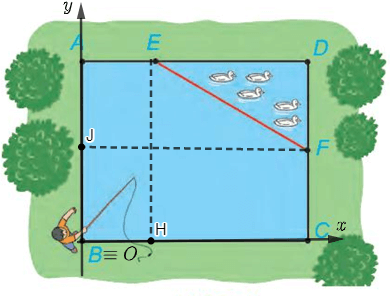
a) Chọn hệ trục tọa độ Oxy, có điểm O trùng với điểm B, các tia Ox, Oy tương ứng trùng với các tia BC, BA. Chọn 1 đơn vị độ dài trên mặt phẳng tọa độ tương ứng với 1 m trong thực tế. Hãy xác định tọa độ của các điểm A, B, C, D, E, F và viết phương trình đường thẳng EF. 

b) Nam đứng ở vị trí B câu cá và có thể quăng lưỡi câu xa 10,7 m. Hỏi lưỡi câu có thể rơi vào nơi nuôi vịt hay không ? 

Lời giải:

a) Đặt hệ trục tọa độ như hình vẽ sau: 

Vì B trùng với gốc tọa độ O nên B có tọa độ là (0; 0). 

Vì ABCD là hình chữ nhật nên CD = AB = 12 m, BC = AD = 15 m. 

Điểm A thuộc trục Oy và có AO = AB = 12 m nên A có tọa độ là (0; 12). 

Điểm C thuộc trục Ox và có CO = CB = 15 m nên C có tọa độ là (15; 0). 

Ta có: DC ⊥ Ox (do DC ⊥ BC), DA ⊥ Oy (do DA ⊥ AB) và DC = 12 m, DA = 15 m nên điểm D có tọa độ là (15; 12). 

Từ E kẻ EH vuông góc với BC, H thuộc BC nên EH = AB = 12 m, lại có AE = 5 m, do đó điểm E có tọa độ là (5; 12).

Từ F kẻ FJ vuông góc với AB, J thuộc AB nên FJ = AD = 15 m, lại có CF = 6 m, do đó điểm F có tọa độ là (15; 6). 

Vậy A(0; 12), B(0; 0), C(15; 0), D(15; 12), E(5; 12), F(15; 6). 

Ta có: $\overrightarrow{EF}=\left(15-5;6-12\right)=\left(10;-6\right)$. 

Chọn vectơ $\overrightarrow{u}=\frac{1}{2}\overrightarrow{EF}=\left(5;-3\right)$ làm vectơ chỉ phương của đường thẳng EF thì vectơ pháp tuyến của đường thẳng EF là $\overrightarrow{n}=\left(3;5\right)$. 

Đường thẳng EF đi qua điểm E(5; 12) và có một vectơ pháp tuyến là $\overrightarrow{n}=\left(3;5\right)$, do đó phương trình đường thẳng EF là: 3(x – 5) + 5(y – 12) = 0 hay 3x + 5y – 75 = 0. 

b) Áp dụng công thức tính khoảng cách, ta có khoảng cách từ B đến EF là: 

$d\left(B,EF\right)=\frac{\left|3.0+5.0-75\right|}{\sqrt{3^2+5^2}}=\frac{75}{\sqrt{34}}$≈ 12,9 m. 

Khoảng cách từ B đến EF là đường ngắn nhất từ B nơi Nam đứng đến EF, lưỡi câu có thể quăng xa 10,7 m và 10,7 m < 12,9 m nên lưỡi câu không thể rơi vào vị trí nuôi vịt. 

Lời giải bài tập Toán 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách hay, chi tiết khác:

• Mở đầu trang 36 Toán 10 Tập 2: Trong mặt phẳng tọa độ, mỗi đường thẳng đều có đối tượng đại số tương ứng, gọi là phương trình của nó ....

• HĐ1 trang 36 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho hai đường thẳng ∆₁: x – 2y + 3 = 0, ∆₂: 3x – y – 1 = 0 ....

• Luyện tập 1 trang 37 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau ....

• HĐ2 trang 37 Toán 10 Tập 2: Hai đường thẳng ∆₁ và ∆₂ cắt nhau tạo thành bốn góc (H.7.6). Các số đo của bốn góc đó có mối quan hệ gì với nhau? ....

• HĐ3 trang 38 Toán 10 Tập 2: Cho hai đường thẳng cắt nhau ∆₁, ∆₂ tương ứng có các vectơ pháp tuyến ....

• Luyện tập 2 trang 38 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ∆₁: x + 3y + 2 = 0 và ∆₂: y = 3x + 1 ....

• Luyện tập 3 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ${\Delta }_1:\left\{\begin{array}{l}x=2+t\\ y=1-2t\end{array}\right.$và ${\Delta }_2:\left\{\begin{array}{l}x=1+t^{\text{'}}\\ y=5+3t^{\text{'}}\end{array}\right.$ ....

• Luyện tập 4 trang 39 Toán 10 Tập 2: Cho đường thẳng ∆: y = ax + b với a ≠ 0 ....

• HĐ4 trang 40 Toán 10 Tập 2: Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến ....

• Trải nghiệm trang 40 Toán 10 Tập 2: Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ (H.7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả ....

• Luyện tập 5 trang 40 Toán 10 Tập 2: Tính khoảng cách từ điểm M(1; 2) đến đường thẳng $\Delta :\left\{\begin{array}{l}x=5+3t\\ y=-5-4t\end{array}\right.$ ....

• Bài 7.7 trang 41 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau: ∆₁:$3\sqrt{2}x+\sqrt{2}y-\sqrt{3}=0$....

• Bài 7.8 trang 41 Toán 10 Tập 2: Tính góc giữa các cặp đường thẳng sau: $∆1: \sqrt{3x} + y – 4 = 0$....

• Bài 7.9 trang 41 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho điểm A(0; – 2) và đường thẳng ∆: x + y – 4 = 0 ....

• Bài 7.10 trang 41 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(– 2; – 1) ....

• Bài 7.11 trang 41 Toán 10 Tập 2: Chứng minh rằng hai đường thẳng d: y = ax + b (a ≠ 0) và d': y = a'x + b' (a' ≠ 0) vuông góc với nhau khi và chỉ khi aa' = – 1 ....

• Bài 7.12 trang 41 Toán 10 Tập 2: Trong mặt phẳng tọa độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu ....