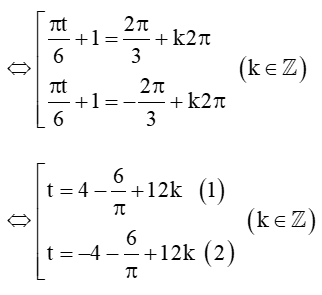Bài 13 trang 42 Toán 11 Tập 1 Cánh diều

❮ Bài trước Bài sau ❯

Hằng ngày, mực nước của một con kênh lên xuống theo thuỷ triều. Độ sâu h(m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày (0 ≤ t < 24) cho bởi công thức h = 3cos+12 (). Tìm t để độ sâu của mực nước là:

Giải Toán 11 Bài tập cuối chương 1 - Cánh diều

Bài 13 trang 42 Toán 11 Tập 1: Hằng ngày, mực nước của một con kênh lên xuống theo thuỷ triều. Độ sâu h(m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày (0 ≤ t < 24) cho bởi công thức h = 3cos $(\frac{π t}{6} + 1)$ +12 (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2021). Tìm t để độ sâu của mực nước là:

a) 15 m;

b) 9 m;

c) 10,5 m.

Lời giải:

a) Để độ sâu của mực nước là 15 m thì:

h = 3cos $(\frac{π t}{6} + 1)$ +12 = 15

$\Leftrightarrow \cos (\frac{π t}{6} + 1) = 1$

$\Leftrightarrow \frac{π t}{6} + 1 = k 2 π (k \in ℤ)$

$\Leftrightarrow t = - \frac{6}{π} + 12 k (k \in ℤ)$

Do 0 ≤ t < 24 nên $0 \leq - \frac{6}{π} + 12 k < 24$

$\Leftrightarrow \frac{6}{π} \leq 12 k < 24 + \frac{6}{π}$

$\Leftrightarrow \frac{1}{2 π} \leq k < 2 + \frac{1}{2 π}$

Mà k ∈ ℤ nên k ∈ {1; 2}.

Với k = 1 thì $t = - \frac{6}{π} + 12.1 \approx 10, 09$ (giờ);

Với k = 2 thì $t = - \frac{6}{π} + 12.2 \approx 22, 09$ (giờ).

Vậy lúc 10,09 giờ và 22,09 giờ thì mực nước có độ sâu là 15 m.

b) Để độ sâu của mực nước là 9 m thì:

h = 3cos $(\frac{π t}{6} + 1)$ +12 = 9

$\Leftrightarrow \cos (\frac{π t}{6} + 1) = - 1$

$\Leftrightarrow \frac{π t}{6} + 1 = π + k 2 π (k \in ℤ)$

$\Leftrightarrow t = 6 - \frac{6}{π} + 12 k (k \in ℤ)$

Do 0 ≤ t < 24 nên $0 \leq 6 - \frac{6}{π} + 12 k < 24$

$\Leftrightarrow - 6 + \frac{6}{π} \leq 12 k < 18 + \frac{6}{π}$

$\Leftrightarrow - \frac{1}{2} + \frac{1}{2 π} \leq k < \frac{3}{2} + \frac{1}{2 π}$

Mà k ∈ ℤ nên k ∈ {0; 1}.

Với k = 0 thì $t = 6 - \frac{6}{π} + 12.0 \approx 4, 09$ (giờ);

Với k = 1 thì $t = 6 - \frac{6}{π} + 12.1 \approx 16, 09$ (giờ).

Vậy lúc 4,09 giờ và 16,09 giờ thì mực nước có độ sâu là 9 m.

c) Để độ sâu của mực nước là 10,5 m thì:

h = 3cos $(\frac{π t}{6} + 1)$ +12 = 10,5

$\Leftrightarrow \cos (\frac{π t}{6} + 1) = - \frac{1}{2}$

Bài 13 trang 42 Toán 11 Tập 1 | Cánh diều Giải Toán 11

• Do 0 ≤ t < 24 nên từ (1) ta có: $0 \leq 4 - \frac{6}{π} + 12 k < 24$

$\Leftrightarrow - 4 + \frac{6}{π} \leq 12 k < 20 + \frac{6}{π}$

$\Leftrightarrow - \frac{1}{3} + \frac{1}{2 π} \leq k < \frac{5}{3} + \frac{1}{2 π}$

Mà k ∈ ℤ nên k ∈ {0; 1}.

Với k = 0 thì $t = 4 - \frac{6}{π} + 12.0 \approx 2, 09$ (giờ);

Với k = 1 thì $t = 4 - \frac{6}{π} + 12.1 \approx 14, 09$ (giờ).

• Do 0 ≤ t < 24 nên từ (2) ta có: $0 \leq - 4 - \frac{6}{π} + 12 k < 24$

$\Leftrightarrow 4 + \frac{6}{π} \leq 12 k < 28 + \frac{6}{π}$

$\Leftrightarrow \frac{1}{3} + \frac{1}{2 π} \leq k < \frac{7}{3} + \frac{1}{2 π}$

Mà k ∈ ℤ nên k ∈ {1; 2}.

Với k = 1 thì $t = - 4 - \frac{6}{π} + 12.1 \approx 6, 09$ (giờ);

Với k = 2 thì $t = - 4 - \frac{6}{π} + 12.2 \approx 18, 09$ (giờ).

Vậy lúc 2,09 giờ, 6,09 giờ, 14,09 giờ và 18,09 giờ thì mực nước có độ sâu là 10,5 m.

Lời giải bài tập Toán 11 Bài tập cuối chương 1 hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán 11 Cánh diều

Bài 13 trang 42 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài tập cuối chương 1 - Cánh diều

Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác: