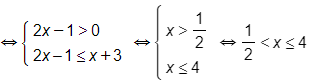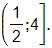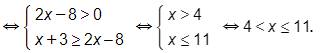Giải Toán 11 trang 55 Tập 2 Cánh diều

---

Với Giải Toán 11 trang 55 Tập 2 trong Bài 4: Phương trình, bất phương trình mũ và lôgarit Toán lớp 11 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 55.

Giải Toán 11 trang 55 Tập 2 Cánh diều

Bài 2 trang 55 Toán 11 Tập 2: Giải mỗi bất phương trình sau:

a) $3^x>\frac{1}{243};$                                          b) ${\left(\frac{2}{3}\right)}^{3x-7}\le \frac{3}{2};$

c) 4^x+3 ≥ 32^x;                                         d) log(x – 1) < 0;

e) ${\log }_{\frac{1}{5}}\left(2x-1\right)\ge {\log }_{\frac{1}{5}}\left(x+3\right);$                g) ln(x + 3) ≥ ln(2x – 8).

Lời giải:

a) $3^x>\frac{1}{243}\iff x>{\log }_3\frac{1}{243}\iff x>{\log }_3\frac{1}{3^5}\iff x>{\log }_3{3}^{-5}\iff x>-5$

Vậy bất phương trình đã cho có tập nghiệm là (–5; +∞).

b) ${\left(\frac{2}{3}\right)}^{3x-7}\le \frac{3}{2}\iff 3x-7\ge {\log }_{\frac{2}{3}}\frac{3}{2}$

$\iff 3x-7\ge {\log }_{\frac{2}{3}}{\left(\frac{2}{3}\right)}^{-1}\iff 3x-7\ge -1\iff x\ge 2.$

Vậy bất phương trình đã cho có tập nghiệm là [2; +∞).

c) 4^x+3 ≥ 32^x ⇔ x + 3 ≥ log₄32^x ⇔ x + 3 ≥ xlog₄32

$\iff x+3\ge xlo{g}_{2^2}{2}^5\iff x+3\ge x\cdot \frac{1}{2}\cdot 5\cdot lo{g}_{2}2$

$\iff x+3\ge \frac{5}{2}x\iff \frac{-3}{2}x\ge -3\iff x\le 2.$

Vậy bất phương trình đã cho có tập nghiệm là (−∞; 2].

d) log(x – 1) < 0 ⇔0 < x – 1 < 10⁰

⇔0 < x – 1 < 1 ⇔1 < x < 2

Vậy bất phương trình đã cho có tập nghiệm là (1; 2).

e) ${\log }_{\frac{1}{5}}\left(2x-1\right)\ge {\log }_{\frac{1}{5}}\left(x+3\right)$

Vậy bất phương trình đã cho có tập nghiệm là 

g) ln(x + 3) ≥ ln(2x – 8)

Vậy bất phương trình đã cho có tập nghiệm là (4; 11].

Bài 3 trang 55 Toán 11 Tập 2: Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất x% / năm (x > 0). Sau 3 năm, người đó rút được cả gốc và lãi là 119,1016 triệu đồng. Tìm x, biết rằng lãi suất không thay đổi qua các năm và người đó không rút tiền ra trong suốt quá trình gửi.

Lời giải:

Công thức tính số tiền rút được (cả gốc và lãi) sau n năm là: 100(1 + x%)ⁿ (triệu đồng).

Sau 3 năm, người đó rút được cả gốc và lãi là 119,1016 triệu đồng nên ta có:

100(1 + x%)³ = 119,1016

$\iff {\left(1+\frac{x}{100}\right)}^3=\mathrm{1,191016}$

$\iff 1+\frac{x}{100}=\sqrt[3]{\mathrm{1,191016}}=\mathrm{1,06}$

 $\iff \frac{x}{100}=\mathrm{0,06}\iff x=6$ (thỏa mãn x > 0).

Vậy lãi xuất là 6% / năm.

Bài 4 trang 55 Toán 11 Tập 2: Sử dụng công thức tính mức cường độ âm L ở Ví dụ 14, hãy tính mức cường độ âm mà tai người có thể chịu đựng được, biết rằng giá trị cực đại của mức cường độ âm mà tai người có thể chịu đựng được là 130dB.

Lời giải:

Ta có công thức tính mức cường độ âm L (đơn vị dB) là $L=10\log \frac{I}{{10}^{-12}}$

Do giá trị cực đại của mức cường độ âm mà tai người có thể chịu đựng được là 130dB nên ta có L ≤ 130

$\iff 10\log \frac{I}{{10}^{-12}}\le 130\iff \log \frac{I}{{10}^{-12}}\le 13$

$\iff \frac{I}{{10}^{-12}}\le {10}^{13}\iff I\le {10}^{13}{.10}^{-12}\iff I\le 10$

Vậy cường độ âmmà tai người có thể chịu đựng được là 10 W/m².

Lời giải bài tập Toán 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit Cánh diều hay khác:

• Giải Toán 11 trang 48

• Giải Toán 11 trang 49

• Giải Toán 11 trang 50

• Giải Toán 11 trang 51

• Giải Toán 11 trang 52

• Giải Toán 11 trang 53

• Giải Toán 11 trang 54