Bài 5 trang 70 Toán 11 Tập 1 Chân trời sáng tạo

Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:

Giải Toán 11 Bài 1: Giới hạn của dãy số - Chân trời sáng tạo

Bài 5 trang 70 Toán 11 Tập 1: Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:

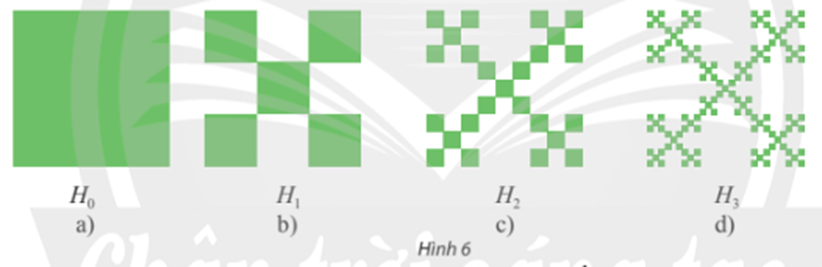
a) Bắt đầu một hình vuông H­₀ cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông H₀ thành chín hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình H₁ (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của H₁ thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình H₂ (xem Hình 6c). Tiếp tục quá trình này ta nhận được một dãy hình H_n(n = 1, 2, 3, ...).

Ta có: H₁ có 5 hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3}$;

H₂ có 5.5 = 5² hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3}.\frac{1}{3}=\frac{1}{3^2};\mathrm{...}$

Từ đó, nhận được H_n có 5ⁿ hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3^n}$.

a) Tính diện tích S_n của H_n và tính lim S_n.

b) Tính chu vi p_n của H_n và tính limp_n.

(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích lim S_n và chu vi limp_n).

Lời giải:

a) Diện tích S_n của H_n là $S_n=5^n.{\left(\frac{1}{3}\right)}^n.{\left(\frac{1}{3}\right)}^n=5^n.{\left(\frac{1}{3}\right)}^{2n}={\left(\frac{5}{9}\right)}^n$

Khi đó ${\text{limS}}_n=\lim {\left(\frac{5}{9}\right)}^n=0$.

b) Chu vi p_n của H_n là: $p_n=5^n.\left(4.\frac{1}{3^n}\right)=4.{\left(\frac{5}{3}\right)}^n$.

Khi đó limp_n = lim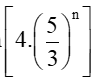 = 0.

Lời giải bài tập Toán 11 Bài 1: Giới hạn của dãy số hay, chi tiết khác:

• Hoạt động khởi động trang 64 Toán 11 Tập 1: Bạn nam thứ 1: Số thập phân vô hạn tuần hoàn 0,666... và số $\frac{2}{3}$ là hai số bằng nhau ....

• Hoạt động khám phá 1 trang 64 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{{\left(-1\right)}^n}{n}$ ....

• Thực hành 1 trang 65 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim \frac{1}{n^2}$ ....

• Hoạt động khám phá 2 trang 65 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{2n+1}{n}$ ....

• Thực hành 2 trang 65 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim \left(2+{\left(\frac{2}{3}\right)}^n\right)$ ....

• Hoạt động khám phá 3 trang 66 Toán 11 Tập 1: Ở trên ta đã biết $\lim \left(3+\frac{1}{n^2}\right)=\lim \frac{3n^2+1}{n^2}=1$ ....

• Thực hành 3 trang 66 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim \frac{2n^2+3n}{n^2+1}$ ....

• Hoạt động khám phá 4 trang 67 Toán 11 Tập 1: Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông ....

• Thực hành 4 trang 68 Toán 11 Tập 1: Tính tổng của cấp số nhân lùi vô hạn: $1+\frac{1}{3}+{\left(\frac{1}{3}\right)}^2+\mathrm{...}+{\left(\frac{1}{3}\right)}^n+\mathrm{...}$ ....

• Vận dụng 1 trang 68 Toán 11 Tập 1: Từ tờ giấy, cắt một hình tròn bán kính R (cm) như Hình 3a ....

• Hoạt động khám phá 5 trang 68 Toán 11 Tập 1: Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4 ....

• Bài 1 trang 69 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim \frac{-2n+1}{n}$ ....

• Bài 2 trang 69 Toán 11 Tập 1: Tính tổng của các cấp số nhân lùi vô hạn sau: a) $-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\mathrm{...}+{\left(-\frac{1}{2}\right)}^n+\mathrm{...}$ ....

• Bài 3 trang 69 Toán 11 Tập 1: Viết số thập phân vô hạn tuần hoàn 0,444 ... dưới dạng phân số ....

• Bài 4 trang 70 Toán 11 Tập 1: Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai ....