Hoạt động khám phá 5 trang 68 Toán 11 Tập 1 Chân trời sáng tạo

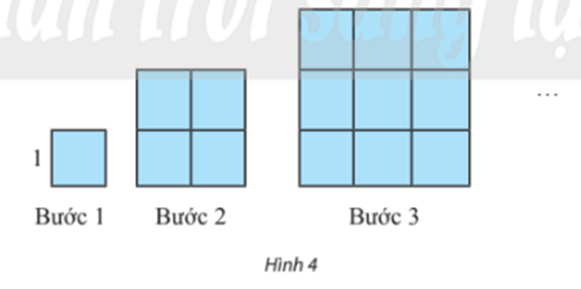
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu u (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ n.

Giải Toán 11 Bài 1: Giới hạn của dãy số - Chân trời sáng tạo

Hoạt động khám phá 5 trang 68 Toán 11 Tập 1: Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu u_n (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ n.

a) Với n như thế nào thì u_n vượt quá 10 000; 1 000 000?

b) Cho hình có diện tích S. Với n như thế nào thì u_n vượt quá S?

Lời giải:

a) Diện tích của hình vuông u_n dựng ở bước thứ n là: u_n = n² (đơn vị diện tích).

Để u_n vượt quá 10 000 thì n² > 10 000 ⇔ n > 100.

Để u_n vượt quá 1 000 000 thì n² > 1 000 000 ⇔ n > 1000.

b) Để u_n vượt quá S thì u_n > S ⇔ n² > S ⇔ n > $\sqrt{S}$.

Lời giải bài tập Toán 11 Bài 1: Giới hạn của dãy số hay, chi tiết khác:

• Hoạt động khởi động trang 64 Toán 11 Tập 1: Bạn nam thứ 1: Số thập phân vô hạn tuần hoàn 0,666... và số $\frac{2}{3}$ là hai số bằng nhau ....

• Hoạt động khám phá 1 trang 64 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{{\left(-1\right)}^n}{n}$ ....

• Thực hành 1 trang 65 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim \frac{1}{n^2}$ ....

• Hoạt động khám phá 2 trang 65 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{2n+1}{n}$ ....

• Thực hành 2 trang 65 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim \left(2+{\left(\frac{2}{3}\right)}^n\right)$ ....

• Hoạt động khám phá 3 trang 66 Toán 11 Tập 1: Ở trên ta đã biết $\lim \left(3+\frac{1}{n^2}\right)=\lim \frac{3n^2+1}{n^2}=1$ ....

• Thực hành 3 trang 66 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim \frac{2n^2+3n}{n^2+1}$ ....

• Hoạt động khám phá 4 trang 67 Toán 11 Tập 1: Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông ....

• Thực hành 4 trang 68 Toán 11 Tập 1: Tính tổng của cấp số nhân lùi vô hạn: $1+\frac{1}{3}+{\left(\frac{1}{3}\right)}^2+\mathrm{...}+{\left(\frac{1}{3}\right)}^n+\mathrm{...}$ ....

• Vận dụng 1 trang 68 Toán 11 Tập 1: Từ tờ giấy, cắt một hình tròn bán kính R (cm) như Hình 3a ....

• Bài 1 trang 69 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim \frac{-2n+1}{n}$ ....

• Bài 2 trang 69 Toán 11 Tập 1: Tính tổng của các cấp số nhân lùi vô hạn sau: a) $-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\mathrm{...}+{\left(-\frac{1}{2}\right)}^n+\mathrm{...}$ ....

• Bài 3 trang 69 Toán 11 Tập 1: Viết số thập phân vô hạn tuần hoàn 0,444 ... dưới dạng phân số ....

• Bài 4 trang 70 Toán 11 Tập 1: Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai ....

• Bài 5 trang 70 Toán 11 Tập 1: Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau: ....