Bài 7.31 trang 63 Toán 11 Tập 2 - Kết nối tri thức

Giải Toán 11 Bài 27. Thể tích - Kết nối tri thức

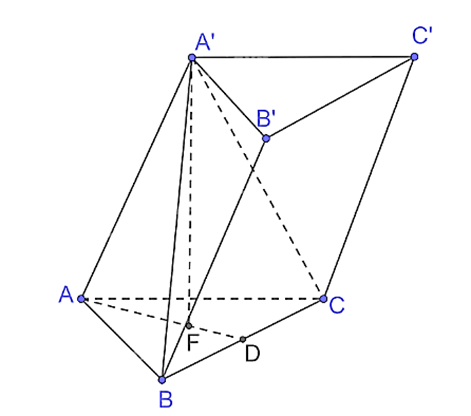
Bài 7.31 trang 63 Toán 11 Tập 2: Cho khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a, A'A = A'B = A'C = b. Tính thể tích của khối lăng trụ.

Lời giải:

Bài 7.31 trang 63 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Vì hình chóp A'.ABC có A'A = A'B = A'C, ABC là tam giác đều nên hình chóp A'.ABC là hình chóp đều.

Gọi F là hình chiếu của A' trên mặt phẳng (ABC), khi đó F là trọng tâm tam giác ABC. Khi đó A'F $⊥$ (ABC) hay A'F là đường cao của hình lăng trụ ABC.A'B'C'.

Giả sử AF $\cap$ CB tại D, suy ra D là trung điểm của BC, AD $⊥$ BC.

Vì ABC là tam giác đều cạnh a, đường cao AD nên AD = $\frac{a \sqrt{3}}{2}$ và S_{ABC = $\frac{a^{2} \sqrt{3}}{4}$} .

Có AF = $\frac{2}{3}$ AD = $\frac{2}{3}$ . $\frac{a \sqrt{3}}{2}$ = $\frac{a \sqrt{3}}{3}$ .

Xét tam giác A'FA vuông tại F, có

A'F = $\sqrt{A {A^{'}}^{2} - A F^{2}} = \sqrt{b^{2} - \frac{a^{2}}{3}} = \sqrt{\frac{3 b^{2} - a^{2}}{3}}$ .

Khi đó $V_{A B C . A^{'} B^{'} C^{'}} = S_{A B C} \cdot A^{'} F$ $= \frac{a^{2} \sqrt{3}}{4} \cdot \sqrt{\frac{3 b^{2} - a^{2}}{3}}$ $= \frac{a^{2} \sqrt{3 b^{2} - a^{2}}}{4}$ .

Lời giải bài tập Toán 11 Bài 27. Thể tích hay, chi tiết khác:

Giải Toán 11 Kết nối tri thức

Bài 7.31 trang 63 Toán 11 Tập 2 - Kết nối tri thức

Giải Toán 11 Bài 27. Thể tích - Kết nối tri thức

Xem thêm lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác: