Bài 8.25 trang 80 Toán 11 Tập 2 - Kết nối tri thức
Hai chuyến bay của hai hãng hàng không X và Y, hoạt động độc lập với nhau. Xác suất để chuyến bay của hãng X và hãng Y khởi hành đúng giờ tương ứng là 0,92 và 0,98.
Giải Toán 11 Bài tập cuối chương 8 - Kết nối tri thức
Bài 8.25 trang 80 Toán 11 Tập 2: Hai chuyến bay của hai hãng hàng không X và Y, hoạt động độc lập với nhau. Xác suất để chuyến bay của hãng X và hãng Y khởi hành đúng giờ tương ứng là 0,92 và 0,98.
Dùng sơ đồ hình cây, tính xác suất để:
a) Cả hai chuyến bay khởi hành đúng giờ;
b) Chỉ có một chuyến bay khởi hành đúng giờ;
c) Có ít nhất một trong hai chuyến bay khởi hành đúng giờ.
Lời giải:
Gọi biến cố A: “Chuyến bay của hãng X khởi hành đúng giờ”, biến cố B: “Chuyến bay của hãng Y khởi hành đúng giờ”. Từ giả thiết, ta có hai biến cố A và B độc lập.
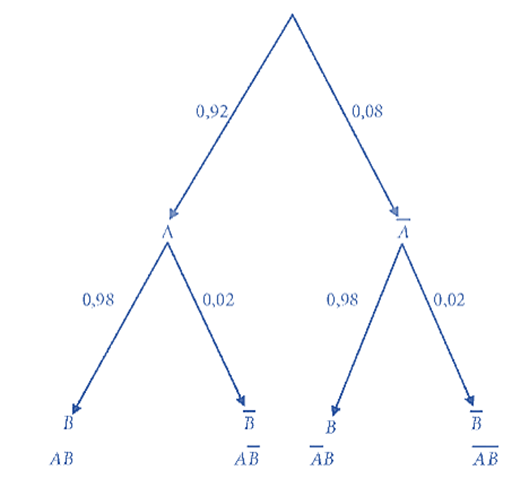
Ta có sơ đồ hình cây để mô tả như sau:
Theo sơ đồ hình cây, ta có:
a) P(AB) = P(A) . P(B) = 0,92 . 0,98 = 0,9016.
Vậy xác suất để cả hai chuyến bay khởi hành đúng giờ là 0,9016.
b) P(A∪B) = P(A) + P(B) = 0,92 . 0,02 + 0,08 . 0,98 = 0,0968.
Vậy xác suất để chỉ có một chuyến bay khởi hành đúng giờ 0,0968.
c) P() = 0,08 . 0,02 = 0,0016
Suy ra P(A ∪ B) = 1 – P() = 1 – 0,0016 = 0,9984.
Vậy xác suất để có ít nhất một trong hai chuyến bay khởi hành đúng giờ là 0,9984.
Lời giải bài tập Toán 11 Bài tập cuối chương 8 hay, chi tiết khác:
Bài 8.16 trang 79 Toán 11 Tập 2: Một hộp đựng 20 tấm thẻ cùng loại được đánh số từ 1 đến 20 ....
Bài 8.17 trang 79 Toán 11 Tập 2: Một hộp đựng 20 tấm thẻ cùng loại được đánh số từ 1 đến 20 ....
Bài 8.18 trang 79 Toán 11 Tập 2: Tại một hội thảo quốc tế có 50 nhà khoa học, trong đó có 31 ....