Luyện tập 1 trang 77 Toán 11 Tập 2 - Kết nối tri thức
Các học sinh lớp 11D làm thí nghiệm gieo hai loại hạt giống A và B. Xác suất để hai loại hạt giống A và B nảy mầm tương ứng là 0,92 và 0,88. Giả sử việc nảy mầm của hạt A và hạt B là độc lập với nhau. Dùng sơ đồ hình cây tính xác suất để:
Giải Toán 11 Bài 30: Công thức nhân xác suất cho hai biến cố độc lập - Kết nối tri thức
Luyện tập 1 trang 77 Toán 11 Tập 2: Các học sinh lớp 11D làm thí nghiệm gieo hai loại hạt giống A và B. Xác suất để hai loại hạt giống A và B nảy mầm tương ứng là 0,92 và 0,88. Giả sử việc nảy mầm của hạt A và hạt B là độc lập với nhau. Dùng sơ đồ hình cây tính xác suất để:
a) Hạt giống A nảy mầm còn hạt giống B không nảy mầm;
b) Hạt giống A không nảy mầm còn hạt giống B nảy mầm;
c) Ít nhất có một trong hai loại hạt giống nảy mầm.
Lời giải:
Gọi A là biến cố “Hạt giống A nảy mầm”; B là biến cố “Hạt giống B nảy mầm”.
Các biến cố đối là biến cố “Hạt giống A không nảy mầm”; là “Hạt giống B không nảy mầm”.
Ta có:
P(A) = 0,92. Suy ra P() = 1 – 0,92 = 0,08.
P(B) = 0,88. Suy ra P() = 1 – 0,88 = 0,12.
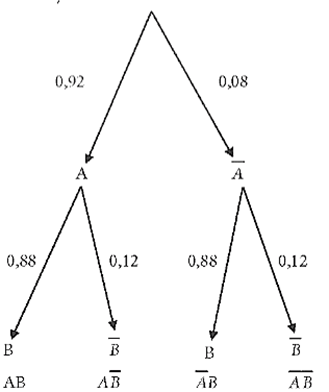
Ta có sơ đồ hình cây như sau:
Ta có hai biến cố A và B độc lập.
a)
Biến cố: “Hạt giống A nảy mầm còn hạt giống B không nảy mầm” là biến cố A.
Áp dụng công thức nhân xác suất, ta có:
P(A) = P(A) . P() = 0,92 . 0,12 = 0,1104.
b)
Biến cố: “Hạt giống A không nảy mầm còn hạt giống B nảy mầm” là biến cố B.
Áp dụng công thức nhân xác suất, ta có:
P(B) = P() . P(B) = 0,08 . 0,88 = 0,0704.
c)
Biến cố: “Có ít nhất một trong hai loại hạt giống nảy mầm” là biến cố A ∪ B.
Áp dụng công thức cộng xác suất và công thức nhân xác suất, ta có:
P(A ∪ B) = P(A) + P(B) – P(AB)
= P(A) + P(B) – P(A) . P(B)
= 0,92 + 0,88 – 0,92 . 0,88
= 0,9904.
Vậy P(A ∪ B) = 0,9904.
Lời giải bài tập Toán 11 Bài 30: Công thức nhân xác suất cho hai biến cố độc lập hay, chi tiết khác:
Mở đầu trang 76 Toán 11 Tập 2: Tại vòng chung kết của một đại hội thể thao, vận động viên An ....
HĐ1 trang 76 Toán 11 Tập 2: Có hai hộp đựng các quả bóng có cùng kích thước và khối lượng ....