Giải Toán 11 trang 23 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 23 Tập 2 trong Bài 21: Phương trình, bất phương trình mũ và lôgarit Toán lớp 11 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 23.

Giải Toán 11 trang 23 Tập 2 Kết nối tri thức

Luyện tập 3 trang 23 Toán 11 Tập 2: Giải các bất phương trình sau:

a) 0,1^{2x – 1} ≤ 0,1^{2 – x};

b) 3 ∙ 2^{x + 1} ≤ 1.

Lời giải:

a) Ta có:

0,1^{2x – 1} ≤ 0,1^{2 – x}

⇔ 2x – 1 ≥ 2 – x (do 0 < 0,1 < 1)

⇔ 3x ≥ 3

⇔ x ≥ 1.

Vậy tập nghiệm của bất phương trình đã cho là [1; + ∞).

b) 3 ∙ 2^{x + 1} ≤ 1

$\iff 2^{x+1}\le \frac{1}{3}$

$\iff x+1\le {\log }_2\frac{1}{3}$ (do 2 > 1)

⇔ x ≤ log₂3^{– 1} – 1

⇔ x ≤ – log₂3 – log₂2

⇔ x ≤ – log₂(3 ∙ 2)

⇔ x ≤ – log₂6

Vậy tập nghiệm của bất phương trình đã cho là (– ∞; – log₂6].

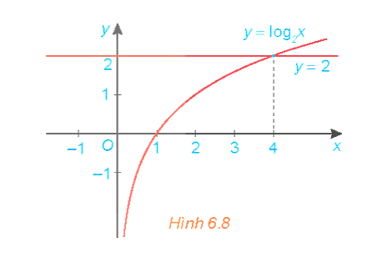
HĐ4 trang 23 Toán 11 Tập 2: Nhận biết nghiệm của bất phương trình lôgarit

Cho đồ thị của các hàm số y = log₂x và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số y = log₂x nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình log₂ x > 2.

Lời giải:

Quan sát đồ thị ở Hình 6.8, ta thấy khoảng giá trị của x mà đồ thị hàm số y = log₂x nằm phía trên đường thẳng y = 2 là (4; + ∞).

Vậy tập nghiệm của bất phương trình log₂ x > 2 là (4; + ∞).

Lời giải bài tập Toán 11 Bài 21: Phương trình, bất phương trình mũ và lôgarit Kết nối tri thức hay khác:

• Giải Toán 11 trang 20
• Giải Toán 11 trang 21
• Giải Toán 11 trang 24