Giải Toán 11 trang 30 Tập 2 Kết nối tri thức

---

Với Giải Toán 11 trang 30 Tập 2 trong Bài 22: Hai đường thẳng vuông góc Toán lớp 11 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 30.

Giải Toán 11 trang 30 Tập 2 Kết nối tri thức

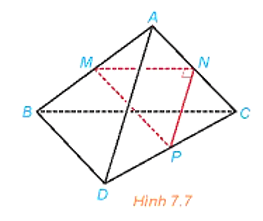
Luyện tập trang 30 Toán 11 Tập 2: Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Chứng minh rằng AD và BC vuông góc với nhau và chéo nhau.

Lời giải:

Xét tam giác ABC có M là trung điểm của AB, N là trung điểm của AC nên MN là đường trung bình của tam giác ABC, suy ra MN // BC.

Xét tam giác ACD có N là trung điểm của AC, P là trung điểm của CD nên NP là đường trung bình của tam giác ACD, suy ra NP // AD.

Khi đó (AD, BC) = (NP, MN) = $\widehat{MNP}$.

Do tam giác MNP vuông tại N nên $\widehat{MNP}=90°$.

Vậy AD và BC vuông góc với nhau.

Nếu D Î (ABC) thì A Î (MNP) (vô lí).

Do đó D Ï (ABC) nên AD và BC chéo nhau.

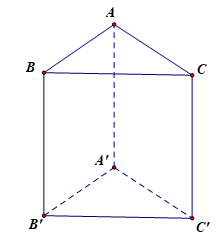
Bài 7.1 trang 30 Toán 11 Tập 2: Cho hình lăng trụ ABC.A'B'C' có đáy là các tam giác đều. Tính góc (AB, B'C').

Lời giải:

Do ABC.A'B'C' là hình lăng trụ nên các mặt bên là hình bình hành.

Do ABB'A' là hình bình hành nên AB // A'B'.

Khi đó (AB, B'C') = (A'B', B'C') = $\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}$.

Do tam giác A'B'C' là tam giác đều nên $\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=60°$.

Vậy (AB, B'C') = 60°.

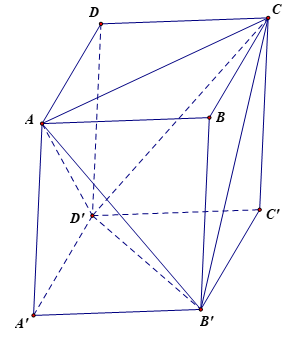
Bài 7.2 trang 30 Toán 11 Tập 2: Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau. Chứng minh rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.

Lời giải:

Vì hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau nên các mặt của hình hộp là hình thoi.

Vì ABB'A' là hình thoi nên AB' ^ A'B.

Có CB // A'D' và CB = A'D' (do cùng song song và bằng AD). Do đó CBA'D' là hình bình hành, suy ra CD' // BA'.

Khi đó (CD', AB') = (BA', AB') = 90°.

Vậy CD' và AB' vuông góc với nhau.

Vì ADD'A' là hình thoi nên AD' ^ A'D.

Có CD // A'B' và CD = A'B' (vì CD, A'B' cùng song song và bằng AB) nên CDA'B' là hình bình hành, suy ra CB' // DA'.

Khi đó (CB', AD') = (DA', AD') = 90°.

Vậy CB' và AD' vuông góc với nhau.

Do ABCD là hình thoi nên AC ^ BD.

Vì BB' // DD' và BB' = DD' (do BB', DD' cùng song song và bằng AA' ) nên BDD'B' là hình bình hành, suy ra BD // B'D'.

Khi đó (AC, B'D') = (AC, BD) = 90°.

Vậy AC và B'D' vuông góc với nhau.

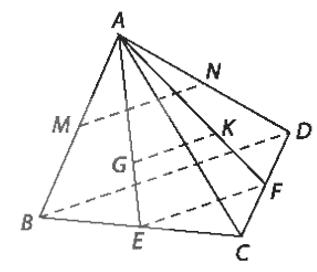
Bài 7.3 trang 30 Toán 11 Tập 2: Cho tứ diện ABCD có $\widehat{CBD}=90°$.

a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc với BC.

b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng GK vuông góc với BC.

Lời giải:

a) Xét tam giác ABD, có M là trung điểm của AB, N là trung điểm của AD nên MN là đường trung bình của tam giác ABD, suy ra MN // BD.

Khi đó (MN, BC) = (BD, BC) = $\widehat{CBD}=90°$.

Vậy MN vuông góc với BC.

b) Gọi AG cắt BC tại E, suy ra E là trung điểm BC, AK cắt CD tại F, suy ra F là trung điểm CD.

Vì G là trọng tâm tam giác ABC nên $\frac{AG}{AE}=\frac{2}{3}$, K là trọng tâm tam giác ACD nên $\frac{AK}{AF}=\frac{2}{3}$.

Xét tam giác AEF có $\frac{AG}{AE}=\frac{AK}{AF}=\frac{2}{3}$ nên GK // EF.

Xét tam giác BCD có E, F lần lượt là trung điểm của BC, CD nên EF là đường trung bình, suy ra EF // BD.

Vì GK // EF và EF // BD nên GK // BD mà BD ^ BC nên GK ^ BC.

Bài 7.4 trang 30 Toán 11 Tập 2: Đối với nhà gỗ truyền thống, trong các cấu kiện: hoành, quá giang, xà cái, rui, cột tương ứng được đánh số 1, 2, 3, 4, 5 như trong Hình 7.8, những cặp cấu kiện nào vuông góc với nhau?

Lời giải:

Những cặp đường thẳng sau vuông góc với nhau: hoành (1) và quá giang (2); hoành (1) và rui (4); hoành (1) và cột (5); quá giang (2) và xà cái (3); quá giang (2) và cột (5); xà cái (3) và rui (4); xà cái (3) và cột (5).

Lời giải bài tập Toán 11 Bài 22: Hai đường thẳng vuông góc Kết nối tri thức hay khác:

• Giải Toán 11 trang 28

• Giải Toán 11 trang 29