Giải Toán 11 trang 34 Tập 2 Kết nối tri thức
Với Giải Toán 11 trang 34 Tập 2 trong Bài 23: Đường thẳng vuông góc với mặt phẳng Toán lớp 11 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 34.
Giải Toán 11 trang 34 Tập 2 Kết nối tri thức
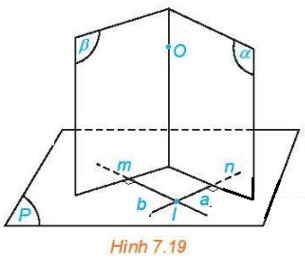
HĐ4 trang 34 Toán 11 Tập 2: Cho mặt phẳng (P) và điểm O. Trong mặt phẳng (P), lấy hai đường thẳng cắt nhau a, b tuỳ ý. Gọi (α), (β) là các mặt phẳng qua O và tương ứng vuông góc với a, b (H.7.19).
a) Giải thích vì sao hai mặt phẳng (α), (β) cắt nhau theo một đường thẳng ∆ đi qua O.
b) Nêu nhận xét về mối quan hệ giữa ∆ và (P).
Lời giải:
a) Vì a ^ (a) nên a và (a) có điểm chung, do đó (a) và (P) có điểm chung.
Mặt khác (a) không trùng (P) vì (a) vuông góc với a và a nằm trong (P). Do đó (a) và (P) cắt nhau theo một giao tuyến n.
Vì b ^ (b) nên b và (b) có điểm chung, do đó (b) và (P) có điểm chung.
Lại có (b) không trùng với (P) vì (b) vuông góc với b và b nằm trong (P). Do đó (b) và (P) cắt nhau theo giao tuyến m.
Do m ^ b, n ^ a và a, b cắt nhau nên m, n cắt nhau suy ra chúng phân biệt.
Do đó, (a) và (b) không thể trùng nhau. Mặt khác, (a) và (b) có điểm chung O nên chúng cắt nhau theo một đường thẳng D đi qua O.
b) Vì (a) và (b) đều đi qua O nên giao tuyến D của chúng đi qua O. Hơn nữa a, b tương ứng vuông góc với (a) và (b) nên chúng vuông góc với D. Do D vuông góc với a, b nên D vuông góc (P).
Luyện tập 2 trang 34 Toán 11 Tập 2: Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Lời giải:
Theo đề có AB ^ (P) và AC ^ (P).
Mà có duy nhất một đường thẳng đi qua A và vuông góc với (P) nên AB và AC trùng nhau. Do đó A, B, C thẳng hàng.
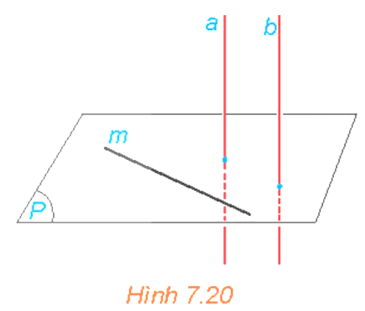
HĐ5 trang 34 Toán 11 Tập 2: Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b. Lấy một đường thẳng m bất kì thuộc mặt phẳng (P) (H.7.20). Tính (b, m) và từ đó rút ra mối quan hệ giữa b và (P).
Lời giải:
Vì a ^ (P) mà m Ì (P) nên a ^ m hay (a, m) = 90°.
Mà b // a nên (b, m) = (a, m) = 90°.
Do b vuông góc với mọi đường thẳng m bất kì trong (P) nên b vuông góc với (P).
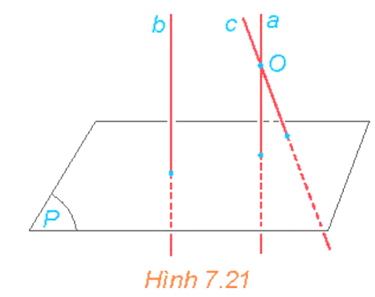
HĐ6 trang 34 Toán 11 Tập 2: Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b (H.7.21).
a) Hỏi c có vuông góc với với (P) hay không ? Nêu nhận xét về vị trí tương đối giữa a và c.
b) Nêu nhận xét về vị trí tương đối giữa hai đường thẳng a và b.
Lời giải:
a) Vì b ⊥ (P) và c // b nên c ⊥ (P).
Vì a và c cắt nhau tại O, mà a ⊥ (P) và c ⊥ (P) nên a và c trùng nhau.
b) Vì a và c trùng nhau và b // c nên a // b.
Lời giải bài tập Toán 11 Bài 23: Đường thẳng vuông góc với mặt phẳng Kết nối tri thức hay khác: