Giải Toán 11 trang 52 Tập 2 Kết nối tri thức

---

Với Giải Toán 11 trang 52 Tập 2 trong Bài 25: Hai mặt phẳng vuông góc Toán lớp 11 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 52.

Giải Toán 11 trang 52 Tập 2 Kết nối tri thức

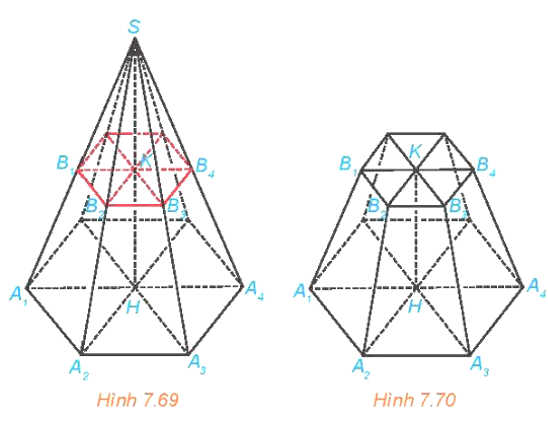
HĐ13 trang 52 Toán 11 Tập 2: Cho hình chóp đều $S.A_1{A}_2\dots A_n$. Một mặt phẳng không đi qua S và song song với mặt phẳng đáy, cắt các cạnh $S{A}_1,S{A}_2,\dots ,S{A}_n$ tương ứng tại $B_1,B_2,\dots ,B_n$ (H.7.69).

a) Giải thích vì sao $S.B_1{B}_2\dots B_n$ là một hình chóp đều.

b) Gọi H là tâm của đa giác $A_1{A}_2\dots A_n$. Chứng minh rằng đường thẳng SH đi qua tâm K của đa giác đều $B_1{B}_2\dots B_n$ và HK vuông góc với các mặt phẳng $\left(A_1{A}_2\dots A_n\right)$, $\left(B_1{B}_2\dots B_n\right)$.

Lời giải:

a) Mặt phẳng không đi qua S và song song với mặt phẳng đáy, cắt các cạnh $S{A}_1,S{A}_2,\dots ,S{A}_n$ tương ứng tại $B_1,B_2,\dots ,B_n$ nên các đa giác A₁A₂…A_n và B₁B₂…B_n có các cạnh tương ứng song song.

Áp dụng định lí Talet trong từng tam giác SA₁A₂; SA₂A₃; …; SA₁A_n, ta được:

$\frac{S{B}_1}{S{A}_1}=\frac{S{B}_2}{S{A}_2}=\mathrm{...}=\frac{S{B}_n}{S{A}_n}$, suy ra $\frac{B_1{B}_2}{A_1{A}_2}=\frac{B_2{B}_3}{A_2{A}_3}=\mathrm{...}=\frac{B_n{B}_1}{A_n{A}_1}$.

Vì đa giác $A_1{A}_2\dots A_n$ đều nên đa giác B₁B₂…B_n đều và SA₁ = SA₂ = … = SA_n nên SB₁ = SB₂ = …= SB_n.

Vậy $S.B_1{B}_2\dots B_n$ là hình chóp đều.

b) Vì H là tâm của đáy $A_1{A}_2\dots A_n$và hình chóp $S.A_1{A}_2\dots A_n$ là hình chóp đều nên

SH ⊥ (A₁A₂…A_n).

Do (A₁A₂…A_n) // (B₁B₂…B_n ) và SH ⊥ (A₁A₂…A_n) nên SH ⊥ (B₁B₂…B_n ).

Hơn nữa, $S.B_1{B}_2\dots B_n$ là hình chóp đều nên SH giao với (B₁B₂…B_n ) tại tâm của đáy B₁B₂…B_n .

Vậy đường thẳng SH đi qua tâm K của đa giác đều $B_1{B}_2\dots B_n$ và HK vuông góc với các mặt phẳng $\left(A_1{A}_2\dots A_n\right)$, $\left(B_1{B}_2\dots B_n\right)$.

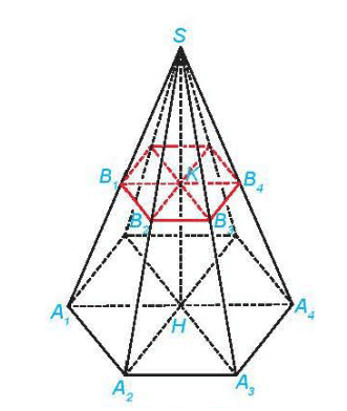
Câu hỏi trang 52 Toán 11 Tập 2: Hình chóp cụt đều có các cạnh bên bằng nhau hay không?

Lời giải:

Hình chóp cụt đều có các cạnh bên bằng nhau vì:

A₁B₁ = SA₁ – SB₁; A₂B₂ = SA₂ – SB₂; …; A_nB_n = SA_n – SB_n.

Dựa vào kết quả của hoạt động 13, ta có: SA₁ = SA₂ = … = SA_n và SB₁ = SB₂ = …= SB_n nên A₁B₁ = A₂B₂ = A_nB_n.

Lời giải bài tập Toán 11 Bài 25: Hai mặt phẳng vuông góc Kết nối tri thức hay khác:

• Giải Toán 11 trang 44

• Giải Toán 11 trang 45

• Giải Toán 11 trang 46

• Giải Toán 11 trang 47

• Giải Toán 11 trang 48

• Giải Toán 11 trang 49

• Giải Toán 11 trang 50

• Giải Toán 11 trang 51

• Giải Toán 11 trang 53