Hoạt động 2 trang 16 Toán 12 Tập 1 Cánh diều

Cho hàm số với x > 1

Giải Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Cánh diều

Hoạt động 2 trang 16 Toán 12 Tập 1: Cho hàm số $f\left(x\right) = x + \frac{1}{x -1}$ với x > 1

a) Tính $\underset{x\to 1^{+}}{\lim f\left(x\right)}$, $\underset{x\to +\infty }{\lim f\left(x\right)}$ .

b) Lập bảng biến thiên của hàm số f(x) trên khoảng (1; + ∞).

c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số f(x) trên khoảng (1; +∞).

Lời giải:

Ta có f(x) =x + $\frac{1}{x - 1} = \frac{x^2 - x +1}{x - 1}$

a) Ta có $\underset{x\to 1^{+}}{\lim }$($x^2 -x + 1)$ = 1 >0,$\underset{x\to 1^{+}}{\lim }$(x - 1) =0 , x – 1 > 0 khi x → 1⁺.

Do đó,$\underset{x\to 1^{+}}{\lim }$f(x) = +$\infty$ .

Ta có $\underset{x\to +\infty }{\lim }$f(x)= $\underset{x\to +\infty }{\lim }$$\frac{x^2-x +1}{x - 1}$= $\underset{x\to +\infty }{\lim }$$\left(x.\frac{1 - {\displaystyle \frac{1}{x}} + {\displaystyle \frac{1}{x^2}}}{1 - {\displaystyle \frac{1}{x}}}\right)$ = $+ \infty$.

b) Ta có f'(x) = 1 - $\frac{1}{{(x -1)}^2}$ với x > 1.

          f'(x) = 0 ⇔ (x – 1)² = 1 ⇔ x = 2 (t/m) hoặc x = 0 (loại).

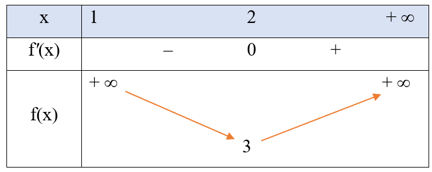
Bảng biến thiên của hàm số f(x) trên khoảng (1; + ∞) như sau:

c) Từ bảng biến thiên ta suy ra hàm số f(x) có giá trị nhỏ nhất trên khoảng (1; + ∞) là 3 tại x = 2 và hàm số này không có giá trị lớn nhất trên khoảng (1; + ∞).

Lời giải bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay, chi tiết khác:

• Câu hỏi khởi động trang 15 Toán 12 Tập 1: Cho một tấm nhôm có dạng hình vuông cạnh 6 dm.Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), ...

• Hoạt động 1 trang 15 Toán 12 Tập 1: Cho hàm số y = f(x) liên tục trên đoạn [– 1; 1] và có đồ thị là đường cong ở Hình 8. ....

• Luyện tập 1 trang 16 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left(x\right) =\sqrt{9 -x^2}$ trên đoạn [– 3; 3].....

• Luyện tập 2 trang 16 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $y = \frac{2x - 5}{x - 1}$ trên nửa khoảng (1; 3].....

• Hoạt động 3 trang 17 Toán 12 Tập 1: Cho hàm số y = f(x) = 2x³ – 6x, x ∈ [– 2; 2] có đồ thị là đường cong ở Hình 9.....

• Luyện tập 3 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = sin 2x – 2x....

• Bài 1 trang 19 Toán 12 Tập 1: Nếu hàm số y = f(x) có đạo hàm trên ℝ thỏa mãn f'(x) = sin x – 2 023, ∀ x ∈ ℝ thì giá trị lớn nhất của hàm số y = f(x) trên đoạn [1; 2] bằng....

• Bài 2 trang 20 Toán 12 Tập 1: Tìm giá trị lớn nhất của mỗi hàm số sau: a) $f\left(x\right) = \frac{4}{1 + x^2}$....

• Bài 3 trang 20 Toán 12 Tập 1: Tìm giá trị nhỏ nhất của mỗi hàm số sau: a) $f\left(x\right) = x + \frac{4}{x}$ trên khoảng (0; + ∞); ....

• Bài 4 trang 20 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau: a) $f\left(x\right) = x^3 -\frac{3}{2}{x}^2$ trên đoạn [– 1; 2];....

• Bài 5 trang 20 Toán 12 Tập 1: Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình ....

• Bài 6 trang 20 Toán 12 Tập 1: Người ta bơm xăng vào bình của một xe ô tô. Biết rằng thể tích V (lít) của lượng xăng trong bình xăng tính theo thời gian bơm xăng t (phút) được cho bởi công thức ....

• Bài 7 trang 20 Toán 12 Tập 1: Ho ép khí quản co lại, ảnh hưởng đến tốc độ của không khí đi vào khí quản. ....