Câu hỏi khởi động trang 15 Toán 12 Tập 1 Cánh diều
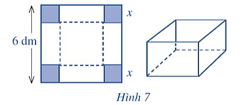
Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), rồi gập tấm nhôm lại như Hình 7 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó.
Giải Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Cánh diều
Câu hỏi khởi động trang 15 Toán 12 Tập 1: Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), rồi gập tấm nhôm lại như Hình 7 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó.
V được tính theo x bởi công thức nào? Có thể tìm giá trị lớn nhất của V bằng cách nào?
Lời giải:
Ta thấy độ dài x (dm) của cạnh hình vuông bị cắt phải thỏa mãn điều kiện 0 < x < 3.
Từ giả thiết suy ra kích thước của khối hộp chữ nhật là x, 6 – 2x, 6 – 2x (dm).
Thể tích của khối hộp là V(x) = x(6 – 2x)2 (dm2) với 0 < x < 3.
Ta phải tìm x0 ∈ (0; 3) sao cho V(x0) có giá trị lớn nhất.
Ta có V'(x) = (6 – 2x)2 – 4x(6 – 2x) = (6 – 2x)(6 – 6x) = 12(3 – x)(1 – x).
Trên khoảng (0; 3), V'(x) = 0 khi x = 1.
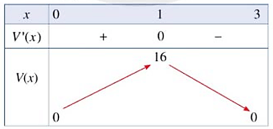
Bảng biến thiên của hàm số V'(x) như sau:
Căn cứ bảng biến thiên, ta thấy: Trên khoảng (0; 3), hàm số V(x) đạt giá trị lớn nhất bằng 16 tại x = 1.
Vậy để khối hộp tạo thành có thể tích lớn nhất thì x = 1 (dm).
Lời giải bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay, chi tiết khác: