Lý thuyết Toán lớp 12 Tính đơn điệu và cực trị của hàm số - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Tính đơn điệu và cực trị của hàm số - Kết nối tri thức

Lý thuyết Tính đơn điệu và cực trị của hàm số

1. Tính đơn điệu của hàm số

•Tính đồng biến, nghịch biến của hàm số

Giả sử K là khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là hàm số xác định trên K.

- Hàm số y = f(x) gọi là đồng biến trên K nếu ∀ x₁, x₂ ∈ K, x₁ < x₂ $\Rightarrow$ f(x₁) < f(x₂).

- Hàm số y = f(x) gọi là nghịch biến trên K nếu ∀ x₁, x₂ ∈ K, x₁ < x₂ $\Rightarrow$ f(x₁) > f(x₂).

Chú ý:

- Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải (H.1.3a).

- Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải (H.1.3b).

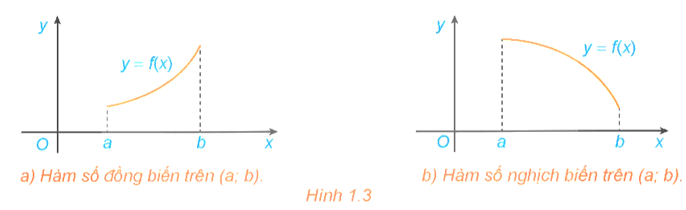
- Hàm số đồng biến hay nghịch biến trên K còn được gọi chung là đơn điệu trên K. Việc tìm các khoảng đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của hàm số.

- Khi xét tính đơn điệu của hàm số mà không chỉ rõ tập K thì ta hiểu là xét trên tập xác định của hàm số đó.

Ví dụ 1. Cho hàm số y = f(x) có đồ thị như hình vẽ. Hãy tìm các khoảng đồng biến, nghịch biến của hàm số.

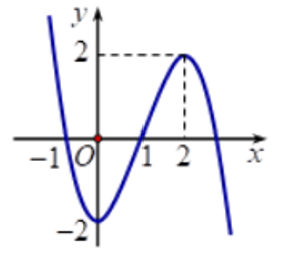
Hướng dẫn giải

Từ đồ thị hàm số, suy ra:

- Hàm số nghịch biến trên các khoảng (−∞; 0) và (2; +∞).

- Hàm số đồng biến trên khoảng (0; 2).

• Tính đơn điệu và dấu của đạo hàm

Cho hàm số y = f(x) có đạo hàm trên khoảng K.

- Nếu f'(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên khoảng K.

- Nếu f'(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên khoảng K.

Chú ý:

- Định lí trên vẫn đúng trong trường hợp f'(x) bằng 0 tại một số hữu hạn điểm trong khoảng K.

- Người ta chứng minh được rằng, nếu f'(x) = 0 với mọi x ∈ K thì hàm số f(x) không đổi trên khoảng K.

Ví dụ 2. Tìm các khoảng đồng biến, nghịch biến của hàm số y = x³ – 2x² + x + 1.

Hướng dẫn giải

Tập xác định của hàm số là ℝ.

Ta có y' = 3x² – 4x + 1.

Ta có y' > 0 khi  $x \in (-\infty ;\frac{1}{3}) \cup (1;+\infty )$ và y' < 0 khi $x\in (\frac{1}{3};1)$  .

Do đó, hàm số đồng biến trên các khoảng $(-\infty ;\frac{1}{3})$ và (1; +∞), nghịch biến trên khoảng $(\frac{1}{3};1)$ .

• Các bước xét tính đơn điệu của hàm số y = f(x)

Bước 1. Tìm tập xác định của hàm số y = f(x).

Bước 2. Tính đạo hàm f'(x). Tìm các điểm x_i (i = 1, 2, …, n) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.

Bước 3. Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên của hàm số.

Bước 4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.

Ví dụ 3. Tìm các khoảng đơn điệu của hàm số $y=\frac{5-2x}{x+3}$ .

Hướng dẫn giải

Tập xác định của hàm số là ℝ\{−3}.

Có $y\text{'}=\frac{(5-2x)\text{'}.(x+3)-(5-2x).(x+3)\text{'}}{{(x+3)}^2}=-\frac{11}{{(x+3)}^2}<0$  với mọi x ≠ −3.

Lập bảng biến thiên của hàm số

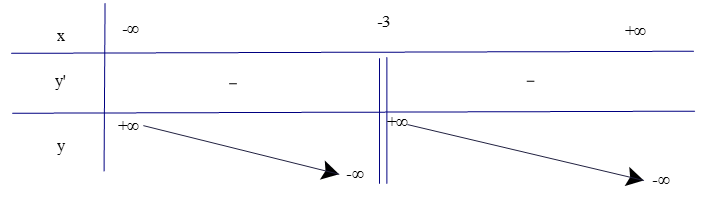
Từ bảng biến thiên, ta có: hàm số nghịch biến trên các khoảng (−∞; −3) và (−3; +∞).

2. Cực trị của hàm số

• Định nghĩa

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (a có thể là −∞, b có thể là +∞) và điểm x₀ ∈ (a; b).

- Nếu tồn tại số h > 0 sao cho f(x) < f(x₀) với mọi x ∈ (x₀ – h; x₀ + h) $\subset$ (a; b) và x ≠ x₀ thì ta nói hàm số f(x) đạt cực đại tại x₀.

- Nếu tồn tại h > 0 sao cho f(x) > f(x₀) với mọi x ∈ (x₀ – h; x₀ + h) $\subset$(a; b) và x ≠ x₀ thì ta nói hàm số f(x) đạt cực tiểu tại x₀.

Chú ý:

- Nếu hàm số y = f(x) đạt cực đại tại x₀ thì x₀ được gọi là điểm cực đại của hàm số f(x). Khi đó, f(x₀) được gọi là giá trị cực đại của hàm số f(x) và kí hiệu f_CĐ hay y_CĐ. Điểm M₀(x₀; f(x₀)) được gọi là điểm cực đại của đồ thị hàm số.

- Nếu hàm số y = f(x) đạt cực tiểu tại x₀ thì x₀ được gọi là điểm cực tiểu của hàm số f(x). Khi đó, f(x₀) được gọi là giá trị cực tiểu của hàm số f(x) và kí hiệu là f_CT hay y_CT. Điểm M₀(x₀; f(x₀)) được gọi điểm cực tiểu của đồ thị hàm số.

- Các điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị) của hàm số.

Ví dụ 4. Cho hàm số có đồ thị như hình vẽ. Hãy tìm các cực trị của hàm số.

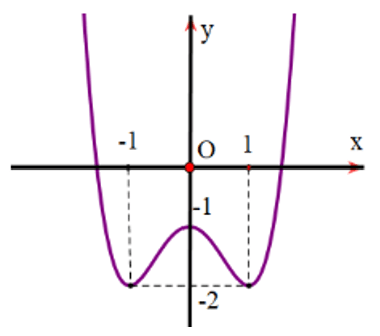
Hướng dẫn giải

Từ đồ thị hàm số, ta có:

Hàm số đạt cực tiểu tại x = −1 và y_CT = y(−1) = −2.

Hàm số đạt cực đại tại x = 0 và y_CĐ = y(0) = −1.

Hàm số đạt cực tiểu tại x = 1 và y_CT = y(1) = −2.

• Mối liên hệ giữa đạo hàm và cực trị

Giả sử hàm số y = f(x) liên tục trên khoảng (a; b) chứa điểm x₀ và có đạo hàm trên các khoảng (a; x₀) và (x₀; b). Khi đó

- Nếu f'(x) < 0 với mọi x ∈ (a; x₀) và f'(x) > 0 với mọi x ∈ (x₀; b) thì x₀ là một điểm cực tiểu của hàm số f(x).

- Nếu f'(x) > 0 với mọi x ∈ (a; x₀) và f'(x) < 0 với mọi x ∈ (x₀; b) thì x₀ là một điểm cực đại của hàm số f(x).

Ví dụ 5. Cho hàm số y = f(x) có bảng biến thiên như sau:

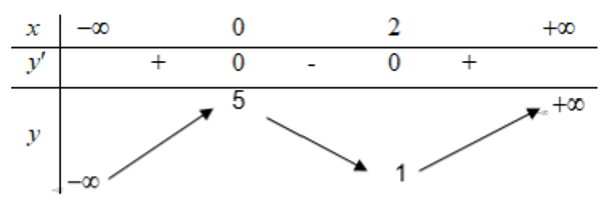
Tìm cực trị của hàm số trên.

Hướng dẫn giải

Dựa vào bảng biến thiên, ta có:

Hàm số đạt cực đại tại x = 0 và y_CĐ  = y(0) = 5.

Hàm số đạt cực tiểu tại x = 2 và y_CT = y(2) = 1.

• Các bước tìm điểm cực trị của hàm số f(x)

Bước 1. Tìm tập xác định của hàm số f(x):

Bước 2. Tính đạo hàm f'(x). Tìm các điểm mà tại đó đạo hàm f'(x) bằng 0 hoặc đạo hàm không tồn tại.

Bước 3. Lập bảng biến thiên của hàm số.

Bước 4.Từ bảng biến thiên suy ra các cực trị của hàm số.

Ví dụ 6. Tìm cực trị của hàm số y = x⁴ – 4x² – 3.

Hướng dẫn giải

Tập xác định của hàm số là ℝ.

Ta có y' = 4x³ – 8x; y' = 0 $\iff$$x=-\sqrt{2}$ hoặc x = 0 hoặc $x=\sqrt{2}$.

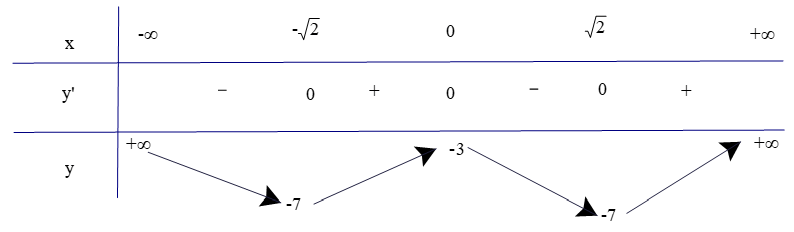
Từ bảng biến thiên, ta có:

- Hàm số đạt cực đại tại x = 0 và y_CĐ = y(0) = −3.

- Hàm số đạt cực tiểu tại $x=-\sqrt{2}$ và $y_{CT} =y(-\sqrt{2} )=-7$ .

- Hàm số đạt cực tiểu tại  $x=\sqrt{2}$ và $y_{CT} =y(\sqrt{2} )=-7$ .

Chú ý:

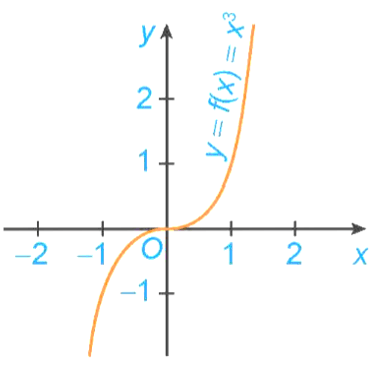
Nếu f'(x₀) = 0 nhưng f'(x) không đổi dấu khi x qua x₀ thì x₀ không phải là điểm cực trị của hàm số. Chẳng hạn, hàm số f(x) = x³ có f'(x) = 3x², f'(0) = 0, nhưng x = 0 không phải là điểm cực trị của hàm số.

Bài tập Tính đơn điệu và cực trị của hàm số

Bài 1. Cho hàm số y = x³ + 3x² – 9x + 15. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số nghịch biến trên khoảng (−3; 1).

B. Hàm số đồng biến trên (−9; −5).

C. Hàm số đồng biến trên ℝ.

D. Hàm số đồng biến trên (5; +∞).

Hướng dẫn giải

Đáp án đúng là: C

Tập xác định: D = ℝ.

Có y' = 3x² + 6x – 9; y' = 0 $\iff$ x = −3 hoặc x = 1.

Bảng biến thiên:

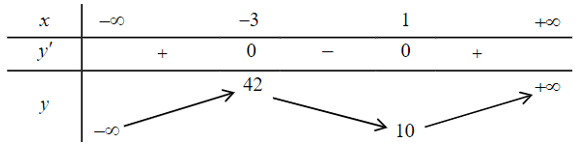
Dựa vào bảng biến thiên, ta có:

Hàm số đồng biến trên cách khoảng (−∞; −3) và (1; +∞).

Hàm số nghịch biến trên khoảng (−3; 1).

Bài 2. Hàm số y = x⁴ – 2x² + 1 có bao nhiêu điểm cực trị?

A. 2.                             B. 3.                                      C. 1.                                                                           D. 0.

Hướng dẫn giải

Đáp án đúng là: B

Tập xác định: D = ℝ.

Có y' = 4x³ – 4x; y' = 0 $\iff$ x = −1 hoặc x = 0 hoặc x = 1.

Bảng biến thiên

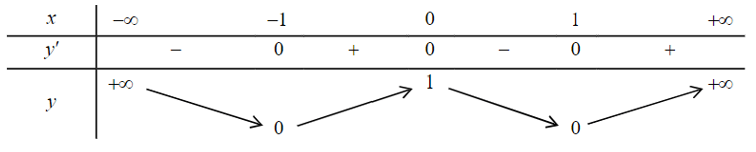
Dựa vào bảng biến thiên, ta có:

Hàm số đạt cực tiểu tại x = ±1 và y_CT = 0.

Hàm số đạt cực đại tại x = 0 và y_CĐ = 1.

Bài 3. Tìm các khoảng đơn điệu của các hàm số sau

a) y = x³ – 3x;                                                   b) $y=\frac{2x-1}{x-1}$.

Hướng dẫn giải

a) Tập xác định: D = ℝ.

Có y' = 3x² – 3; y' = 0$\iff$x = 1 hoặc x = −1.

Bảng biến thiên

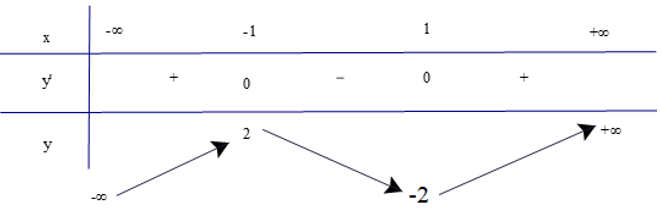
Dựa vào bảng biến thiên, ta có

Hàm số đồng biến trên các khoảng (−∞; −1) và (1; +∞).

Hàm số nghịch biến trên khoảng (−1; 1).

b) Tập xác định: D = ℝ\{1}.

Có $y\text{'}=\frac{2(x-1)-(2x-1)}{{(x-1)}^2}=\frac{-1}{{(x-1)}^2}<0,\forall x\ne 1$ .

Do đó hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).

Bài 4. Tìm cực trị của các hàm số sau

a) $y=\frac{2x+3}{x+1}$;                                                   b) y = 2x⁴ – 4x² + 2022.

Hướng dẫn giải

a) Tập xác định: D = ℝ\{−1}.

Có $y\text{'}=\frac{2(x+1)-(2x+3)}{{(x+1)}^2}=\frac{-1}{{(x+1)}^2}<0,\forall x\ne -1$.

Do đó hàm số không có cực trị.

b) Tập xác định: D = ℝ.

Có y' = 8x³ – 8x; y' = 0 $\iff$ x = −1 hoặc x = 0 hoặc x = 1.

Bảng biến thiên

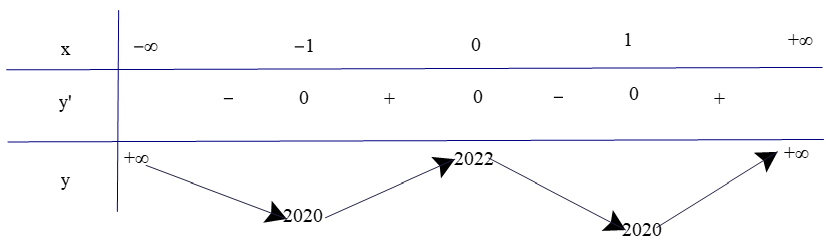
Dựa vào bảng biến thiên ta có:

Hàm số đạt cực đại tại x = 0 và y_CĐ = 2022.

Hàm số đạt cực tiểu tại x = ±1 và y_CT = 2020.

Bài 5. Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức G(x) = 0,024x²(30 – x), trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp (x được tính bằng mg). Tìm lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.

Hướng dẫn giải

Tập xác định: D = (0; 30).

Có G'(x) = 0,048x(30 – x) – 0,024x² = 0,024x(60 – 3x);

G'(x) = 0 $\iff$ x = 0 hoặc x = 20.

Bảng biến thiên

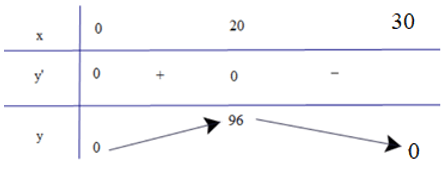
Dựa vào bảng biến thiên, ta có lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất là x = 20 mg.

Học tốt Tính đơn điệu và cực trị của hàm số

Các bài học để học tốt Tính đơn điệu và cực trị của hàm số Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số