Lý thuyết Toán lớp 12 Tích phân - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 12: Tích phân sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Tích phân - Kết nối tri thức

Lý thuyết Tích phân

1. Khái niệm tích phân

• Diện tích hình thang cong

+) Hình thang cong: Hình phẳng giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b, (a < b), trong đó f(x) là hàm liên tục không âm trên đọan [a; b], gọi là một hình thang cong.

+) Diện tích hình thang cong

Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b là S = F(b) – F(a), trong đó F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b].

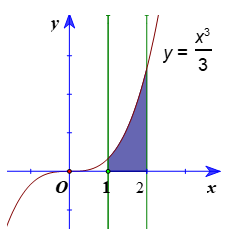
Ví dụ 1. Tính diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x) = $\frac{x^3}{3}$ , trục hoành và hai đường thẳng x = 1, x = 2.

Hướng dẫn giải

Một nguyên hàm của hàm số $f\left(x\right)=\frac{x^3}{3}$  là $F\left(x\right)=\frac{x^4}{12}$ .

Do đó, diện tích của hình thang cong cần tính là:

S = F(2) – F(1) = $\frac{2^4}{12}-\frac{1^4}{12}=\frac{15}{12}=\frac{5}{4}$ .

• Định nghĩa tích phân

Cho f(x) là hàm số liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b] thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ .

Chú ý

a) Hiệu F(b) – F(a) thường được kí hiệu là $F\left(x\right)|\begin{array}{c}b\\ a\end{array}$ . Như vậy $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=F\left(x\right)|\begin{array}{c}b\\ a\end{array}$ .

b) Ta gọi $\underset{a}{\overset{b}{\int }}$   là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

c) Trong trường hợp a = b hoặc a > b, ta quy ước:

$\underset{a}{\overset{a}{\int }}f\left(x\right)dx=0;\underset{a}{\overset{b}{\int }}f\left(x\right)dx=-\underset{b}{\overset{a}{\int }}f\left(x\right)dx$ .

Ví dụ 2. Tính

a) $\underset{0}{\overset{1}{\int }}4x^{3}dx$ ;                                         b) $\underset{1}{\overset{2}{\int }}{3}^{x}dx$ .

Hướng dẫn giải

a) $\underset{0}{\overset{1}{\int }}4x^{3}dx$$=x^4{|}_0^1=1-0=1$ .

b) $\underset{1}{\overset{2}{\int }}{3}^{x}dx$$=\frac{3^x}{\ln 3}{|}_1^2=\frac{3^2}{\ln 3}-\frac{3}{\ln 3}=\frac{6}{\ln 3}$ .

• Ý nghĩa hình học của tích phân

Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì tích phân $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ là diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b. Vậy S = $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ .

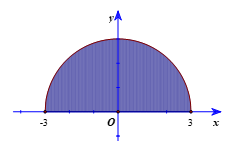
Ví dụ 3. Sử dụng ý nghĩa hình học của tích phân, tính $\underset{-3}{\overset{3}{\int }}\sqrt{9-x^2}dx$ .

Hướng dẫn giải

Ta có $y=\sqrt{9-x^2}$ là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc tọa độ O và bán kính 3. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng.

Vậy $\underset{-3}{\overset{3}{\int }}\sqrt{9-x^2}dx=\frac{1}{2}\pi {.3}^2=\frac{9\pi }{2}$ .

2. Tính chất của tích phân

1) $\underset{a}{\overset{b}{\int }}kf\left(x\right)dx=k\underset{a}{\overset{b}{\int }}f\left(x\right)dx$  (k là hằng số);

2) $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx+\underset{a}{\overset{b}{\int }}g\left(x\right)dx$ ;

3) $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx-\underset{a}{\overset{b}{\int }}g\left(x\right)dx$ ;

4) $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{c}{\int }}f\left(x\right)dx+\underset{c}{\overset{b}{\int }}f\left(x\right)dx$  (a < c < b).

Ví dụ 4. Tính

a) $I=\underset{0}{\overset{1}{\int }}\left(4x^3-e^x\right)dx$ ;                          b) $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(1+\sin x\right)dx$ .

Hướng dẫn giải

a) $I=\underset{0}{\overset{1}{\int }}\left(4x^3-e^x\right)dx$$=\underset{0}{\overset{1}{\int }}4x^{3}dx-\underset{0}{\overset{1}{\int }}{e}^{x}dx$

$=x^4{|}_0^1-e^x{|}_0^1=1-e+1=2-e$ .

b) $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(1+\sin x\right)dx$$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}1dx+\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sin xdx$

$=x{|}_0^{\frac{\pi }{2}}-\cos x{|}_0^{\frac{\pi }{2}}$$=\frac{\pi }{2}+1$ .

Bài tập Tích phân

Bài 1. Biết $\underset{1}{\overset{5}{\int }}f\left(x\right)dx=4$ . Giá trị của $\underset{1}{\overset{5}{\int }}3f\left(x\right)dx$  bằng

A. 7.

B. $\frac{4}{3}$ .

C. 64.

D. 12.

Hướng dẫn giải

Đáp án đúng là: D

Ta có  $\underset{1}{\overset{5}{\int }}3f\left(x\right)dx=3\underset{1}{\overset{5}{\int }}f\left(x\right)dx$= 3.4 = 12.

Bài 2. Biết F(x) = x³ là một nguyên hàm của hàm số f(x) trên ℝ. Giá trị của $\underset{1}{\overset{2}{\int }}\left(2+f\left(x\right)\right)dx$  bằng

A. $\frac{23}{4}$ .

B. 7.

C. 9.

D. $\frac{15}{4}$ .

Hướng dẫn giải

Đáp án đúng là: C

Ta có $\underset{1}{\overset{2}{\int }}\left(2+f\left(x\right)\right)dx$$=\underset{1}{\overset{2}{\int }}2dx+\underset{1}{\overset{2}{\int }}f\left(x\right)dx$

$=2x{|}_1^2+F\left(x\right){|}_1^2$$=2+x^3{|}_1^2$  = 9.

Bài 3. Tính

a) $\underset{0}{\overset{1}{\int }}\left(3x+1\right)\left(x+3\right)dx$ ;                        b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^2\frac{x}{2}dx$ .

Hướng dẫn giải

a)  $\underset{0}{\overset{1}{\int }}\left(3x+1\right)\left(x+3\right)dx$$=\underset{0}{\overset{1}{\int }}\left(3x^2+10x+3\right)dx$

$=\left(x^3+5x^2+3x\right){|}_0^1$= 9.

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^2\frac{x}{2}dx$$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1+\cos x}{2}dx$$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1}{2}dx+\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{\cos x}{2}dx$

$=\frac{1}{2}\left(x+\sin x\right){|}_0^{\frac{\pi }{2}}$$=\frac{1}{2}\left(\frac{\pi }{2}+1\right)$ .

Bài 4. Tính $I=\underset{-2}{\overset{2}{\int }}\left|x^2-1\right|dx$ .

Hướng dẫn giải

$I=\underset{-2}{\overset{2}{\int }}\left|x^2-1\right|dx$$=\underset{-2}{\overset{-1}{\int }}\left|x^2-1\right|dx+\underset{-1}{\overset{1}{\int }}\left|x^2-1\right|dx+\underset{1}{\overset{2}{\int }}\left|x^2-1\right|dx$

$=\underset{-2}{\overset{-1}{\int }}\left(x^2-1\right)dx+\underset{-1}{\overset{1}{\int }}\left(1-x^2\right)dx+\underset{1}{\overset{2}{\int }}\left(x^2-1\right)dx$

$=\left(\frac{x^3}{3}-x\right){|}_{-2}^{-1}+\left(x-\frac{x^3}{3}\right){|}_{-1}^1+\left(\frac{x^3}{3}-x\right){|}_1^2$

$=\frac{2}{3}+\frac{2}{3}+\frac{2}{3}+\frac{2}{3}+\frac{2}{3}+\frac{2}{3}=4$

Bài 5. Cho hai quả bóng A, B di chuyển ngược chiều nhau va chạm với nhau. Sau va chạm mỗi quả bóng nảy ngược lại một đoạn thì dừng hẳn. Biết sau khi va chạm, quả bóng A nảy ngược lại với vận tốc v_A(t) = 8 – 2t (m/s) và quả bóng B nảy ngược lại với vận tốc v_B(t) = 12 – 4t (m/s). Tính khoảng cách giữa hai quả bóng sau khi đã dừng hẳn (giả sử hai quả bóng đều chuyển động thẳng).

Hướng dẫn giải

Thời gian quả bóng A chuyển động từ lúc va chạm đến khi dừng hẳn là

v_A(t) = 0 $\iff$ 8 – 2t = 0 $\iff$ t = 4 (s).

Quãng đường quả bóng A di chuyển là

$S_A=\underset{0}{\overset{4}{\int }}\left(8-2t\right)dt=\left(8t-t^2\right){|}_0^4=16$  (m).

Thời gian quả bóng B chuyển động từ lúc va chạm đến khi dừng hẳn là

v_B(t) = 0 $\iff$ 12 – 4t = 0 $\iff$ t = 3 (s).

Quãng đường quả bóng B đi được là

$S_B=\underset{0}{\overset{3}{\int }}\left(12-4t\right)dt=\left(12t-2t^2\right){|}_0^3=18$  (m).

Khoảng cách giữa hai quả bóng sau khi đã dừng hẳn là:

S = S_A + S_B = 16 + 18 = 34 (m).

Học tốt Tích phân

Các bài học để học tốt Tích phân Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 12: Tích phân