Tổng hợp lý thuyết Toán 12 Chương 5 - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Chương 5: Phương pháp tọa độ trong không gian sách Kết nối tri thức hay nhất, chi tiết với bài tập có lời giải sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm Toán 12 Chương 5.

Tổng hợp lý thuyết Toán 12 Chương 5 - Kết nối tri thức

Lý thuyết tổng hợp Chương 5

1. Phương trình mặt phẳng

1.1. Vectơ pháp tuyến và cặp vectơ chỉ phương của mặt phẳng

• Khái niệm vectơ pháp tuyến

Vectơ $\overrightarrow{n}\ne \overrightarrow{0}$  được gọi là vectơ pháp tuyến của mặt phẳng (α) nếu giá của $\overrightarrow{n}$  vuông góc với (α).

Chú ý

+) Mặt phẳng hoàn toàn xác định khi biết một điểm và một vectơ pháp tuyến của nó.

+) Nếu $\overrightarrow{n}$  là một vectơ pháp tuyến của mặt phẳng (α) thì $k\overrightarrow{n}$  (với k là một số khác 0) cũng là một vectơ pháp tuyến của (α).

• Cách tìm một vectơ vuông góc với hai vectơ cho trước

Trong không gian Oxyz, cho hai vectơ $\overrightarrow{u}=\left(a;b;c\right)$  và $\overrightarrow{v}=\left(a^{\text{'}};b^{\text{'}};c^{\text{'}}\right)$ . Khi đó vectơ $\overrightarrow{n}=\left(b{c}^{\text{'}}-b^{\text{'}}c;c{a}^{\text{'}}-c^{\text{'}}a;a{b}^{\text{'}}-a^{\text{'}}b\right)$ vuông góc với cả hai vectơ $\overrightarrow{u}$  và $\overrightarrow{v}$ , được gọi là tích có hướng của $\overrightarrow{u}$ và $\overrightarrow{v}$, kí hiệu là $\left[\overrightarrow{u},\overrightarrow{v}\right]$ .

Chú ý

+) $\left[\overrightarrow{u},\overrightarrow{v}\right]=\overrightarrow{0}$  khi và chỉ khi $\overrightarrow{u}$, $\overrightarrow{v}$  cùng phương.

+) Với bốn số x, y, x', y', ta kí hiệu $\left|\begin{array}{cc}x& y\\ x^{\text{'}}& y^{\text{'}}\end{array}\right|=x{y}^{\text{'}}-x^{\text{'}}y$ . Khi đó tích có hướng của $\overrightarrow{u}=\left(a;b;c\right)$  và $\overrightarrow{v}=\left(a^{\text{'}};b^{\text{'}};c^{\text{'}}\right)$  là $\left[\overrightarrow{u},\overrightarrow{v}\right]=\left(\left|\begin{array}{cc}b& c\\ b^{\text{'}}& c^{\text{'}}\end{array}\right|;\left|\begin{array}{cc}c& a\\ c^{\text{'}}& a^{\text{'}}\end{array}\right|;\left|\begin{array}{cc}a& b\\ a^{\text{'}}& b^{\text{'}}\end{array}\right|\right)$ .

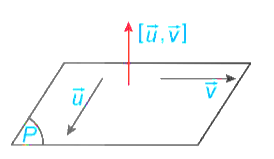
• Khái niệm cặp vectơ chỉ phương của mặt phẳng

+) Trong không gian Oxyz, hai vectơ $\overrightarrow{u},\overrightarrow{v}$  được gọi là cặp vectơ chỉ phương của mặt phẳng (P) nếu chúng không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P).

+) Nếu $\overrightarrow{u},\overrightarrow{v}$  là cặp vectơ chỉ phương của (P) thì $\left[\overrightarrow{u},\overrightarrow{v}\right]$  là một vectơ pháp tuyến của (P).

1.2. Phương trình tổng quát của mặt phẳng

• Khái niệm phương trình tổng quát của mặt phẳng

Trong không gian Oxyz, mỗi mặt phẳng đều có phương trình dạng Ax + By + Cz + D = 0, trong đó A, B, C không đồng thời bằng 0, được gọi là phương trình tổng quát của mặt phẳng đó.

Chú ý. Trong không gian Oxyz, mỗi phương trình Ax + By + Cz + D = 0 (các hệ số A, B, C không đồng thời bằng 0) xác định một mặt phẳng nhận $\overrightarrow{n}=\left(A;B;C\right)$làm một vectơ pháp tuyến.

1.3. Lập phương trình tổng quát của mặt phẳng

• Lập phương trình mặt phẳng đi qua một điểm và biết vectơ pháp tuyến

Trong không gian Oxyz, nếu mặt phẳng (α) đi qua điểm M₀(x₀; y₀; z₀) và có vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right)$thì có phương trình là:

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0 ⇔ Ax + By + Cz + D = 0, với D = −(Ax₀ + By₀ + Cz₀).

• Lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương

Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương $\overrightarrow{u},\overrightarrow{v}$  có thể thực hiện theo các bước sau:

+) Tìm vectơ pháp tuyến $\overrightarrow{n}=\left[\overrightarrow{u},\overrightarrow{v}\right]$ .

+) Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến $\overrightarrow{n}$ .

• Lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng

Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:

+) Tìm cặp vectơ chỉ phương $\overrightarrow{AB},\overrightarrow{AC}$ .

+) Tìm vectơ pháp tuyến $\overrightarrow{n}=\left[\overrightarrow{AB},\overrightarrow{AC}\right]$ .

+) Lập phương trình tổng quát của mặt phẳng đi qua A và có vectơ pháp tuyến $\overrightarrow{n}$ .

1.4. Điều kiện để hai mặt phẳng vuông góc với nhau

Trong không gian Oxyz, cho hai mặt phẳng: (α): Ax + By + Cz + D = 0, (β): A'x + B'y + C'z + D' = 0 với hai vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right),\overrightarrow{n^{\text{'}}}=\left(A^{\text{'}};B^{\text{'}};C^{\text{'}}\right)$tương ứng. Khi đó: (α) $\perp$ (β) $\iff$$\overrightarrow{n}\perp \overrightarrow{n^{\text{'}}}\iff A{A}^{\text{'}}+B{B}^{\text{'}}+C{C}^{\text{'}}=0$ .

1.5. Điều kiện để hai mặt phẳng song song với nhau

Trong không gian Oxyz, cho hai mặt phẳng (α): Ax + By + Cz + D = 0, (β): A'x + B'y + C'z + D' = 0, với các vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right)$, $\overrightarrow{n^{\text{'}}}=\left(A^{\text{'}};B^{\text{'}};C^{\text{'}}\right)$tương ứng. Khi đó: $\left(\alpha \right)//\left(\beta \right)\iff \left\{\begin{array}{l}\overrightarrow{n^{\text{'}}}=k\overrightarrow{n}\\ D^{\text{'}}\ne kD\end{array}\right.$với k nào đó.

Chú ý

+) Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.

+) Hai mặt phẳng (α) và (β) trùng nhau khi và chỉ khi tồn tại số k khác 0 sao cho A' = kA, B' = kB, C' = kC, D' = kD.

16. Khoảng cách từ một điểm đến một mặt phẳng

Trong không gian Oxyz, khoảng cách từ điểm M(x₀; y₀; z₀) đến mặt phẳng (P): Ax + By + Cz + D = 0 là $d\left(M,\left(P\right)\right)=\frac{\left|A{x}_0+B{y}_0+C{z}_0+D\right|}{\sqrt{A^2+B^2+C^2}}$.

2. Phương trình đường thẳng trong không gian

2.1. Phương trình đường thẳng

• Vectơ chỉ phương của đường thẳng

Vectơ $\overrightarrow{u}\ne \overrightarrow{0}$được gọi là vectơ chỉ phương của đường thẳng D nếu giá của $\overrightarrow{u}$song song hoặc trùng với $∆$.

Chú ý

+) Đường thẳng hoàn toàn xác định khi biết một điểm mà nó đi qua và một vectơ chỉ phương.

+) Nếu $\overrightarrow{u}$là một vectơ chỉ phương của $∆$ thì $k\overrightarrow{u}$(với k là một số khác 0) cũng là một vectơ chỉ phương của $∆$.

• Phương trình tham số của đường thẳng

Trong không gian Oxyz, cho đường thẳng $∆$ đi qua điểm A(x₀; y₀; z₀) và có vectơ chỉ phương $\overrightarrow{u}=\left(a;b;c\right)$ . Hệ phương trình $\left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\\ z=z_0+ct\end{array}\right.$  được gọi là phương trình tham số của đường thẳng $∆$ (t là tham số, t $\in$ ℝ).

Chú ý

+) Với các số a, b, c không đồng thời bằng 0, hệ phương trình $\left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\\ z=z_0+ct\end{array}\right.\left(t\in ℝ\right)$  xác định một đường thẳng đi qua điểm M(x₀; y₀; z₀) và có vectơ chỉ phương $\overrightarrow{u}=\left(a;b;c\right)$ .

+) Từ phương trình tham số của đường thẳng, mỗi giá trị của tham số tương ứng với một điểm thuộc đường thẳng và ngược lại.

• Phương trình chính tắc của đường thẳng

Trong không gian Oxyz, cho đường thẳng $∆$ đi qua điểm A(x₀; y₀; z₀) và có vectơ chỉ phương $\overrightarrow{u}=\left(a;b;c\right)$  với a, b, c là các số khác 0.

Hệ phương trình: $\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$  được gọi là phương trình chính tắc của đường thẳng $∆$.

• Phương trình đường thẳng đi qua hai điểm

Trong không gian Oxyz, cho hai điểm phân biệt A₁(x₁; y₁; z₁) và A₂(x₂; y₂; z₂). Đường thẳng A₁A₂ có vectơ chỉ phương $\overrightarrow{A_1{A}_2}=\left(x_2-x_1;y_2-y_1;z_2-z_1\right)$ .

+) Đường thẳng A₁A₂ có phương trình tham số là: $\left\{\begin{array}{l}x=x_1+\left(x_2-x_1\right)t\\ y=y_1+\left(y_2-y_1\right)t\\ z=z_1+\left(z_2-z_1\right)t\end{array}\right.\left(t\in ℝ\right)$ .

+) Trong trường hợp x₁ ≠ x₂, y₁ ≠ y₂, z₁ ≠ z₂ thì đường thẳng A₁A₂ có phương trình chính tắc là: $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$ .

2.2. Hai đường thẳng vuông góc

Trong không gian Oxyz, cho hai đường thẳng $∆$₁, $∆$₂ tương ứng có vectơ chỉ phương $\overrightarrow{u_1}=\left(a_1;b_1;c_1\right)$, $\overrightarrow{u_2}=\left(a_2;b_2;c_2\right)$. Khi đó ${\Delta }_1\perp {\Delta }_2\iff \overrightarrow{u_1}.\overrightarrow{u_2}=0\iff a_1{a}_2+b_1{b}_2+c_1{c}_2=0$.

2.3. Vị trí tương đối giữa hai đường thẳng

Trong không gian Oxyz, cho hai đường thẳng ${∆}_1$, ${∆}_2$ lần lượt đi qua các điểm A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂) và tương ứng có vectơ chỉ phương $\overrightarrow{u_1}=\left(a_1;b_1;c_1\right),\overrightarrow{u_2}=\left(a_2;b_2;c_2\right)$. Khi đó:

+) ${∆}_1$ // ${∆}_2$$\iff$ $\overrightarrow{u_1}$cùng phương với $\overrightarrow{u_2}$và A₁ ${∆}_2$.

+) ${∆}_1$ ≡ ${∆}_2$$\iff$ $\overrightarrow{u_1}$cùng phương với $\overrightarrow{u_2}$và A₁ $\in$ ${∆}_2$.

+) ${∆}_1$ và ${∆}_2$ cắt nhau

$\iff$$\left\{\begin{array}{l}\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\ne \overrightarrow{0}\\ \overrightarrow{A_1{A}_2}\perp \left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\end{array}\right.\iff \left\{\begin{array}{l}\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\ne \overrightarrow{0}\\ \overrightarrow{A_1{A}_2}.\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]=0\end{array}\right.$.

+) ${∆}_1$ và ${∆}_2$ chéo nhau $\iff$ $\overrightarrow{A_1{A}_2}.\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\ne 0$.

Chú ý. Để xét vị trí tương đối giữa hai đường thẳng, ta cũng có thể dựa vào các vectơ chỉ phương và phương trình của hai đường thẳng đó theo tiêu chuẩn sau đây.

Trong không gian Oxyz, cho hai đường thẳng $∆$₁, $∆$₂ tương ứng có vectơ chỉ phương $\overrightarrow{u_1}=\left(a_1;b_1;c_1\right),\overrightarrow{u_2}=\left(a_2;b_2;c_2\right)$và có phương trình tham số:

${\Delta }_1:\left\{\begin{array}{l}x=x_1+a_{1}t\\ y=y_1+b_{1}t\\ z=z_1+c_{1}t\end{array}\right.$; ${\Delta }_2:\left\{\begin{array}{l}x=x_2+a_{2}s\\ y=y_2+b_{2}s\\ z=z_2+c_{2}s\end{array}\right.$

Xét hệ phương trình hai ẩn t, s: $\left\{\begin{array}{l}{x}_1+a_{1}t=x_2+a_{2}s\\ y_1+b_{1}t=y_2+b_{2}s\\ z_1+c_{1}t=z_2+c_{2}s\end{array}\right.$(*).

Khi đó:

+) $∆$₁ // $∆$₂$\iff$ $\overrightarrow{u_1}$cùng phương với $\overrightarrow{u_2}$và hệ (*) vô nghiệm.

+) $∆$₁ ≡ $∆$₂$\iff$ Hệ (*) có vô số nghiệm.

+) $∆$₁ cắt $∆$₂$\iff$ Hệ (*) có nghiệm duy nhất.

+) $∆$₁ và $∆$₂ chéo nhau $\iff$ $\overrightarrow{u_1}$và $\overrightarrow{u_2}$không cùng phương và hệ (*) vô nghiệm.

3. Công thức tính góc trong không gian

3.1. Công thức tính góc giữa hai đường thẳng

Trong không gian Oxyz, cho hai đường thẳng $∆$ và $∆$' tương ứng có vectơ chỉ phương $\overrightarrow{u}=\left(a;b;c\right),\overrightarrow{u^{\text{'}}}=\left(a^{\text{'}};b^{\text{'}};c^{\text{'}}\right)$ . Khi đó:

$\cos \left(\Delta ,{\Delta }^{\text{'}}\right)=\left|\cos \left(\overrightarrow{u},\overrightarrow{u^{\text{'}}}\right)\right|=\frac{\left|a{a}^{\text{'}}+b{b}^{\text{'}}+c{c}^{\text{'}}\right|}{\sqrt{a^2+b^2+c^2}.\sqrt{{a^{\text{'}}}^2+{b^{\text{'}}}^2+{c^{\text{'}}}^2}}$

3.2. Công thức tính góc giữa đường thẳng và mặt phẳng

Trong không gian Oxyz, cho đường thẳng $∆$ có vectơ chỉ phương $\overrightarrow{u}=\left(a;b;c\right)$  và mặt phẳng (P) có vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right)$ . Khi đó:

$\sin \left(\Delta ,\left(P\right)\right)=\left|\cos \left(\overrightarrow{u},\overrightarrow{n}\right)\right|=\frac{\left|aA+bB+cC\right|}{\sqrt{a^2+b^2+c^2}.\sqrt{A^2+B^2+C^2}}$.

3.3. Công thức tính góc giữa hai mặt phẳng

Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là $\overrightarrow{n}=\left(A;B;C\right)$ , $\overrightarrow{n^{\text{'}}}=\left(A^{\text{'}};B^{\text{'}};C^{\text{'}}\right)$ . Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)), được tính theo công thức:

$\cos \left(\left(P\right),\left(Q\right)\right)=\left|\cos \left(\overrightarrow{n},\overrightarrow{n^{\text{'}}}\right)\right|=\frac{\left|A{A}^{\text{'}}+B{B}^{\text{'}}+C{C}^{\text{'}}\right|}{\sqrt{A^2+B^2+C^2}.\sqrt{{A^{\text{'}}}^2+{B^{\text{'}}}^2+{C^{\text{'}}}^2}}$.

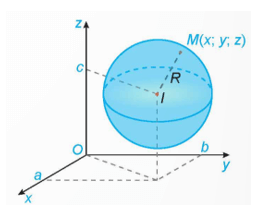
4. Phương trình mặt cầu

Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c) bán kính R có phương trình:

(x – a)² + (y – b)² + (z – c)² = R².

Chú ý

+) Điểm M(x; y; z) nằm trong mặt cầu (S) nếu (x – a)² + (y – b)² + (z – c)² < R².

+) Điểm M(x; y; z) nằm ngoài mặt cầu (S) nếu (x – a)² + (y – b)² + (z – c)² > R².

Nhận xét. Với a, b, c, d là các hằng số, phương trình x² + y² + z² – 2ax – 2by – 2cz + d = 0 có thể viết lại thành (x – a)² + (y – b)² + (z – c)² = a² + b² + c² – d và là phương trình của một mặt cầu (S) khi và chỉ khi a² + b² + c² – d > 0. Khi đó, (S) có tâm I(a; b; c) và bán kính $R=\sqrt{a^2+b^2+c^2-d}$

Bài tập ôn tập Chương 5

1. Bài tập trắc nghiệm

Bài 1. Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c), abc ≠ 0. Khi đó phương trình mặt phẳng (ABC) là:

A. $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$.

B. $\frac{x}{b}+\frac{y}{a}+\frac{z}{c}=1$.

C. $\frac{x}{a}+\frac{y}{c}+\frac{z}{b}=1$.

D. $\frac{x}{c}+\frac{y}{b}+\frac{z}{a}=1$.

Hướng dẫn giải

Đáp án đúng là: A

Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c), abc ≠ 0. Khi đó phương trình mặt phẳng (ABC) là: $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$.

Bài 2. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): 3x + 2y – z + 1 = 0. Mặt phẳng (P) có một vectơ pháp tuyến là:

A. $\overrightarrow{n}=\left(3;2;1\right)$.

B. $\overrightarrow{n}=\left(-2;3;1\right)$.

C. $\overrightarrow{n}=\left(3;2;-1\right)$.

D. $\overrightarrow{n}=\left(3;-2;-1\right)$.

Hướng dẫn giải

Đáp án đúng là: C

Mặt phẳng (α): 3x + 2y – z + 1 = 0 có một vectơ pháp tuyến là $\overrightarrow{n}=\left(3;2;-1\right)$.

Bài 3. Trong không gian Oxyz, cho đường thẳng d: $\frac{x-3}{2}=\frac{y-4}{-5}=\frac{z+1}{3}$. Vectơ nào dưới đây là một vectơ chỉ phương của d?

A. $\overrightarrow{u_2}=\left(2;4;-1\right)$.

B. $\overrightarrow{u_1}=\left(2;-5;3\right)$.

C. $\overrightarrow{u_3}=\left(2;5;3\right)$.

D. $\overrightarrow{u_4}=\left(3;4;1\right)$.

Hướng dẫn giải

Đáp án đúng là: B

Đường thẳng d: $\frac{x-3}{2}=\frac{y-4}{-5}=\frac{z+1}{3}$ có một vectơ chỉ phương là $\overrightarrow{u_1}=\left(2;-5;3\right)$.

Bài 4. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 1; 0) và B(0; 1; 2). Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng AB.

A. $\overrightarrow{u_2}=\left(-1;1;2\right)$.

B. $\overrightarrow{u_1}=\left(-1;0;-2\right)$.

C. $\overrightarrow{u_3}=\left(-1;0;2\right)$.

D. $\overrightarrow{u_4}=\left(1;2;2\right)$.

Hướng dẫn giải

Đáp án đúng là: C

Có $\overrightarrow{AB}=\left(-1;0;2\right)$ . Do đó đường thẳng AB nhận $\overrightarrow{u_3}=\left(-1;0;2\right)$  làm một vectơ chỉ phương.

Bài 5. Trong không gian với hệ tọa độ Oxyz, tính góc giữa hai đường thẳng d₁: $\frac{x}{1}=\frac{y+1}{-1}=\frac{z-1}{2}$  và d₂: $\frac{x+1}{-1}=\frac{y}{1}=\frac{z-3}{1}$ .

A. 45°.

B. 30°.

C. 60°.

D. 90°.

Hướng dẫn giải

Đáp án đúng là: D

Đường thẳng d₁; d₂ lần lượt có vectơ chỉ phương là $\overrightarrow{u}=\left(1;-1;2\right),\overrightarrow{u^{\text{'}}}=\left(-1;1;1\right)$ .

Ta có 

$\cos \left(\Delta ,{\Delta }^{\text{'}}\right)=\left|\cos \left(\overrightarrow{u},\overrightarrow{u^{\text{'}}}\right)\right|=\frac{\left|1.\left(-1\right)+\left(-1\right).1+2.1\right|}{\sqrt{1^2+{\left(-1\right)}^2+2^2}.\sqrt{{\left(-1\right)}^2+1^2+1^2}}=0$

Suy ra ($∆$, $∆$') = 90°.

Bài 6. Trong không gian Oxyz, cho mặt phẳng (P): $-\sqrt{3}x+y+1=0$ . Tính góc tạo bởi (P) với trục Ox?

A. 60°.

B. 30°.

C. 120°.

D. 150°.

Hướng dẫn giải

Đáp án đúng là: A

Mặt phẳng (P) có vectơ pháp tuyến $\overrightarrow{n}=\left(-\sqrt{3};1;0\right)$ .

Trục Ox có vectơ chỉ phương là $\overrightarrow{i}=\left(1;0;0\right)$ .

$\sin \left(Ox,\left(P\right)\right)=\left|\cos \left(\overrightarrow{u},\overrightarrow{n}\right)\right|=\frac{\left|1.\left(-\sqrt{3}\right)\right|}{\sqrt{{\left(-\sqrt{3}\right)}^2+1^2+0^2}.\sqrt{1^2+0^2+0^2}}=\frac{\sqrt{3}}{2}$.

Suy ra (Ox, (P)) = 60°.

Bài 7. Trong không gian Oxyz, cho mặt cầu (S): x² + (y – 2)² + (z + 1)² = 6. Đường kính của (S) bằng

A. $\sqrt{6}$ .

B. 12.

C. $2\sqrt{6}$ .

D. 3.

Hướng dẫn giải

Đáp án đúng là: C

Mặt cầu (S) có bán kính là $\sqrt{6}$ . Suy ra đường kính là $2\sqrt{6}$ .

Bài 8. Trong không gian Oxyz, cho mặt cầu (S): (x – 2)² + (y + 1)² + (z – 3)² = 4. Tâm của (S) có tọa độ là

A. (−2; 1; −3).

B. (−4; 2; −6).

C. (4; −2; 6).

D. (2; −1; 3).

Hướng dẫn giải

Đáp án đúng là: D

Mặt cầu (S) có tâm I(2; −1; 3).

2. Bài tập tự luận

Bài 1. Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(−1; −2; 5) và vuông góc với hai mặt phẳng (Q): x + 2y – 3z + 1 = 0 và (R): 2x – 3y + z + 1 = 0.

Hướng dẫn giải

Mặt phẳng (Q) và (R) có vectơ pháp tuyến lần lượt là

$\overrightarrow{n_Q}=\left(1;2;-3\right),\overrightarrow{n_R}=\left(2;-3;1\right)$

Ta có

$\left[\overrightarrow{n_Q},\overrightarrow{n_R}\right]=\left(\left|\begin{array}{cc}2& -3\\ -3& 1\end{array}\right|;\left|\begin{array}{cc}-3& 1\\ 1& 2\end{array}\right|;\left|\begin{array}{cc}1& 2\\ 2& -3\end{array}\right|\right)=\left(-7;-7;-7\right)$ .

Mặt phẳng (P) đi qua điểm M(−1; −2; 5) nhận $\overrightarrow{n}=\frac{1}{-7}\left[\overrightarrow{n_Q},\overrightarrow{n_R}\right]=\left(1;1;1\right)$  làm một vectơ pháp tuyến có phương trình là: (x + 1) + (y + 2) + (z – 5) = 0 hay x + y + z – 2 = 0.

Bài 2. Trong không gian với hệ tọa độ Oxyz,

a) Viết phương trình mặt phẳng (P) chứa trục Oy và đi qua điểm M(1; 1; −1).

b) Tính khoảng cách từ A(1; 2; 3) đến mặt phẳng (P).

Hướng dẫn giải

a) Trục Oy có vectơ chỉ phương là $\overrightarrow{j}=\left(0;1;0\right)$ , $\overrightarrow{OM}=\left(1;1;-1\right)$ .

Mặt phẳng (P) chứa trục Oy và đi qua điểm M(1; 1; −1) nhận $\overrightarrow{n}=\left[\overrightarrow{j},\overrightarrow{OM}\right]=\left(-1;0;-1\right)$có phương trình là: −1(x – 1) −1(z + 1) = 0 hay x + z = 0.

b) $d\left(A,\left(P\right)\right)=\frac{\left|1+3\right|}{\sqrt{1^2+1^2}}=\frac{4}{\sqrt{2}}=2\sqrt{2}$.

Bài 3. Một công trình đang xây dựng được gắn hệ trục Oxyz (đơn vị trên mỗi trục tọa độ là mét). Ba bức tường (P), (Q), (R) (như hình vẽ) của tòa nhà lần lượt có phương trình (P): x + 2y – 2z + 1 = 0, (Q): 2x + y + 2z – 3 = 0, (R): 2x + 4y – 4z – 19 = 0.

a) Hãy kiểm tra tính song song hoặc vuông góc giữa các bức tường (P), (Q), (R) của tòa nhà.

b) Tính khoảng cách giữa hai bức tường (P) và (R) của tòa nhà.

Hướng dẫn giải

a) Vectơ pháp tuyến của các mặt phẳng (P), (Q), (R) lần lượt là

$\overrightarrow{n_P}=\left(1;2;-2\right),\overrightarrow{n_Q}=\left(2;1;2\right),\overrightarrow{n_R}=\left(2;4;-4\right)$ .

Có $\overrightarrow{n_Q}.\overrightarrow{n_R}=2.2+1.4+2.\left(-4\right)=0$ . Do đó (Q) $\perp$ (R).

Có $\left\{\begin{array}{l}\overrightarrow{n_R}=2\overrightarrow{n_P}\\ -19\ne 2.1\end{array}\right.$  nên (P) // (R).

b) Lấy A(−1; 0; 0) $\in$ (P).

Vì (P) // (R) nên d((P),

d((P),(R)) = d(A, (R)) = $\frac{\left(2.\left(-1\right)+4.0-4.0-19\right)}{\sqrt{2^2+4^2+4^2}}=\frac{21}{6}=\frac{7}{2}$ .

Bài 4. Viết phương trình tham số và phương trình chính tắc của đường thẳng $∆$ trong các trường hợp sau:

a) $∆$ đi qua điểm A(−1; −3; 4) và có vectơ chỉ phương $\overrightarrow{u}=\left(3;5;7\right)$.

b) $∆$ đi qua điểm A(−2; 2; 1) và vuông góc với mặt phẳng (α): x + 2y – 3z + 4 = 0.

Hướng dẫn giải

a) Đường thẳng $∆$ đi qua điểm A(−1; −3; 4) và có vectơ chỉ phương $\overrightarrow{u}=\left(3;5;7\right)$ có phương trình tham số là $\left\{\begin{array}{l}x=-1+3t\\ y=-3+5t\\ z=4+7t\end{array}\right.$và phương trình chính tắc là $\frac{x+1}{3}=\frac{y+3}{5}=\frac{z-4}{7}$.

b) Có $\overrightarrow{n_{\alpha }}=\left(1;2;-3\right)$.

Vì $∆$$\perp$ (α) nên đường thẳng $∆$ nhận $\overrightarrow{u}=\overrightarrow{n_{\alpha }}=\left(1;2;-3\right)$làm một vectơ chỉ phương.

Đường thẳng $∆$ đi qua điểm A(−2; 2; 1), có $\overrightarrow{u}=\left(1;2;-3\right)$làm một vectơ pháp tuyến có phương trình tham số là $\left\{\begin{array}{l}x=-2+t\\ y=2+2t\\ z=1-3t\end{array}\right.$và phương trình chính tắc là $\frac{x+2}{1}=\frac{y-2}{2}=\frac{z-1}{-3}$.

Bài 5. Cho hai đường thẳng d₁: $\left\{\begin{array}{l}x=-2+3t\\ y=-1\\ z=4-t\end{array}\right.$và d₂: $\frac{x-10}{-1}=\frac{y+1}{-1}=\frac{z}{-2}$.

Chứng minh rằng d₁ và d₂ cắt nhau. Tìm tọa độ giao điểm của d₁ và d₂.

Hướng dẫn giải

Đường thẳng d₂ có phương trình tham số là $\left\{\begin{array}{l}x=10-t\\ y=-1-t\\ z=-2t\end{array}\right.$ .

Xét hệ phương trình $\left\{\begin{array}{l}-2+3t=10-t\\ -1=-1-t^{\text{'}}\\ 4-t=-2t^{\text{'}}\end{array}\right.$$\iff \left\{\begin{array}{l}t=4\\ t^{\text{'}}=0\end{array}\right.$ .

Hệ có nghiệm duy nhất. Do đó d₁ và d₂ cắt nhau.

Với t = 4 thay vào phương trình đường thẳng d₁ ta có $\left\{\begin{array}{l}x=10\\ y=-1\\ z=0\end{array}\right.$.

Vậy tọa độ giao điểm của hai đường thẳng là (10; −1; 0).

Bài 6. Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10; 3; 0) và chuyển động đều theo đường cáp có vectơ chỉ phương là $\overrightarrow{u}=\left(2;-2;1\right)$. Viết phương trình chính tắc của đường cáp.

Hướng dẫn giải

Phương trình chính tắc của đường cáp là $\frac{x-10}{2}=\frac{y-3}{-2}=\frac{z}{1}$ .

Bài 7. Trong không gian Oxyz, tính góc tạo bởi hai mặt phẳng (P): 2x + 11y – 5z + 3 = 0 và (Q): −x + 2y + z – 5 = 0.

Hướng dẫn giải

Vectơ pháp tuyến của mặt phẳng (P) và (Q) lần lượt là $\overrightarrow{n}=\left(2;11;-5\right),\overrightarrow{n^{\text{'}}}=\left(-1;2;1\right)$ .

Ta có

$\cos \left(\left(P\right),\left(Q\right)\right)=\left|\cos \left(\overrightarrow{n},\overrightarrow{n^{\text{'}}}\right)\right|=\frac{\left|2.\left(-1\right)+11.2+\left(-5\right).1\right|}{\sqrt{2^2+{11}^2+{\left(-5\right)}^2}.\sqrt{{\left(-1\right)}^2+2^2+1^2}}=\frac{15}{30}=\frac{1}{2}$

Suy ra ((P), (Q)) = 60°.

Bài 8. Trong không gian Oxyz, cho mặt phẳng (Q): x – y – 5 = 0, biết hình chiếu của O lên mặt phẳng (P) là H(2; −1; −2). Tính góc tạo bởi hai mặt phẳng (P), (Q).

Hướng dẫn giải

Vì OH $\perp$ (P) nên mặt phẳng (P) nhận $\overrightarrow{OH}=\left(2;-1;-2\right)$  làm vectơ pháp tuyến.

Mặt phẳng (Q) có vectơ pháp tuyến $\overrightarrow{n}=\left(1;-1;0\right)$ .

Ta có 

$\cos \left(\left(P\right),\left(Q\right)\right)=\frac{\left|2.1+\left(-1\right).\left(-1\right)+\left(-2\right).0\right|}{\sqrt{2^2+{\left(-1\right)}^2+{\left(-2\right)}^2}.\sqrt{1^2+{\left(-1\right)}^2+0^2}}=\frac{3}{3\sqrt{2}}=\frac{1}{\sqrt{2}}$

Suy ra ((P), (Q)) = 45°.

Bài 9. Một công ty xây dựng đang thiết kế một tòa nhà mới. Để tối ưu hóa ánh sáng tự nhiên trong tòa nhà, họ cần xác định góc giữa ánh sáng mặt trời (được biểu diễn bằng một đường thẳng) và mặt phẳng của một bức tường kính. Giả sử rằng:

+) Bức tường kính được đặt trong mặt phẳng (α) có phương trình 2x – 3y + z = 5.

+) Tia sáng mặt trời được biểu diễn bởi đường thẳng d có phương trình tham số $\frac{x-1}{2}=\frac{y+2}{-1}=\frac{z-3}{1}$ .

Hãy tính góc giữa đường thẳng d và mặt phẳng (α).

Hướng dẫn giải

Mặt phẳng (α) có vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-3;1\right)$ .

Đường thẳng d có vectơ chỉ phương là $\overrightarrow{u}=\left(2;-1;1\right)$ .

Ta có 

$\sin \left(d,\left(\alpha \right)\right)=\frac{\left|2.2+\left(-3\right).\left(-1\right)+1.1\right|}{\sqrt{2^2+{\left(-3\right)}^2+1^2}.\sqrt{2^2+{\left(-1\right)}^2+1^2}}=\frac{8}{\sqrt{84}}=\frac{4}{\sqrt{21}}$

Suy ra (d, (α)) ≈ 60,8°.

Bài 10. Trong không gian Oxyz, xác định phương trình mặt cầu (S) biết:

a) mặt cầu (S) có tâm A(2; 1; 0), đi qua điểm B(0; 1; 2).

b) mặt cầu (S) có đường kính AB với A(1; 2; 3), B(5; 4; −1).

Hướng dẫn giải

a) Ta có R = AB = $\sqrt{{\left(0-2\right)}^2+{\left(1-1\right)}^2+{\left(2-0\right)}^2}=2\sqrt{2}$ .

Phương trình mặt cầu cần tìm là: (x – 2)² + (y – 1)² + z² = 8.

b) Gọi I(3; 3; 1) là trung điểm của AB,

$R=\frac{AB}{2}=\frac{\sqrt{{\left(5-1\right)}^2+{\left(4-2\right)}^2+{\left(-1-3\right)}^2}}{2}=3$ .

Phương trình mặt cầu cần tìm là: (x – 3)² + (y – 3)² + (z – 1)² = 9.

Bài 11. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x² + y² + z² – 2x – 2y – 2z – 22 = 0 và mặt phẳng (P): 3x – 2y + 6z + 14 = 0. Tính khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (P).

Hướng dẫn giải

Mặt cầu (S) có tâm là I(1; 1; 1).

Có $d\left(I,\left(P\right)\right)=\frac{\left|3.1-2.1+6.1+14\right|}{\sqrt{3^2+{\left(-2\right)}^2+6^2}}=\frac{21}{7}=3$ .

Bài 12. Trong không gian hệ trục tọa độ Oxyz (đơn vị trên mỗi trục là kilômét) một trạm phát sóng rađa của Nga được đặt trên bán đảo Crimea ở vị trí I(−2; 1; −1) và được thiết kế phát hiện máy bay của địch ở khoảng cách tối đa 500 km.

a) Sử dụng phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phủ sóng của rađa trong không gian.

b) Hai chiếc máy bay do thám của Mỹ và Anh đang bay ở vị trí có tọa độ lần lượt là M(−200; 100; −250) và N(350; −100; 300). Hỏi rađa của Nga có thể phát hiện ra hai chiếc máy bay do thám của Mỹ và Anh không?

Hướng dẫn giải

a) Phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phủ sóng của rađa trong không gian là (x + 2)² + (y – 1)² + (z + 1)² = 250000.

b)

Có $\mathrm{IM}=\sqrt{{\left(-200+2\right)}^2+{\left(100-1\right)}^2+{\left(-250+1\right)}^2}\approx 333,18<\mathrm{R}$ .

$\mathrm{IN}=\sqrt{{\left(350+2\right)}^2+{\left(-100-1\right)}^2+{\left(300+1\right)}^2}\approx 474,03<R$.

Vậy rađa của Nga có thể phát hiện ra hai chiếc máy bay do thám của Mỹ và Anh.

Học tốt Toán 12 Chương 5

Các bài học để học tốt Bài tập cuối chương 5 Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài tập cuối chương 5