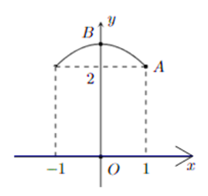Lý thuyết Toán lớp 12 Ứng dụng hình học của tích phân - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 13: Ứng dụng hình học của tích phân sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Ứng dụng hình học của tích phân - Kết nối tri thức

Lý thuyết Ứng dụng hình học của tích phân

1. Ứng dụng tích phân để tính diện tích hình phẳng

• Hình phẳng giới hạn bởi một đồ thị hàm số, trục hoành và hai đường thẳng x = a, x = b.

Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số f(x) liên tục, trục hoành và hai đường thẳng x = a, x = b (a < b), được tính bằng công thức $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$ .

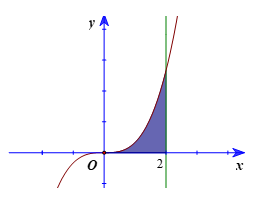
Ví dụ 1. Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số $y=\frac{x^3}{3}$ , trục hoành và hai đường thẳng x = 0; x = 2.

Hướng dẫn giải

Diện tích hình phẳng cần tính là

$S=\underset{0}{\overset{2}{\int }}\left|\frac{x^3}{3}\right|dx$$=\underset{0}{\overset{2}{\int }}\frac{x^3}{3}dx$$=\frac{x^4}{12}{|}_0^2$$=\frac{4}{3}$.

• Hình phẳng giới hạn bởi hai đồ thị hàm số và hai đường thẳng x = a, x = b

Diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a, x = b, được tính bằng công thức $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$ .

Chú ý: Nếu f(x) – g(x) không đổi dấu trên đoạn [a; b] thì

$S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx=\left|\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx\right|$.

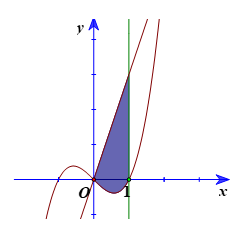
Ví dụ 2. Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y = x³ – x; y = 3x và hai đường thẳng x = 0; x = 1.

Hướng dẫn giải

Diện tích hình phẳng cần tính là

$S=\underset{0}{\overset{1}{\int }}\left|x^3-x-3x\right|dx$$=\underset{0}{\overset{1}{\int }}\left|x^3-4x\right|dx$$=\underset{0}{\overset{1}{\int }}\left(-x^3+4x\right)dx$

$=\left(-\frac{x^4}{4}+2x^2\right){|}_0^1$$=\frac{7}{4}$

2. Ứng dụng tích phân để tính thể tích vật thể

• Tính thể tích vật thể

Cho một vật thể trong không gian Oxyz. Gọi ẞ là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ x = a, x = b. Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích là S(x). Giả sử S(x) là hàm liên tục trên đoạn [a; b]. Khi đó thể tích V của phần vật thể ẞ được tính bởi công thức $V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx$.

Ví dụ 3. Tính thể tích vật thể nằm giữa hai mặt phẳng x = 1 và x = 4, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1 ≤ x ≤ 4) là một tam giác đều cạnh là $\sqrt{x}-1$.

Hướng dẫn giải

Diện tích thiết diện S(x) là

$S\left(x\right)=\frac{\sqrt{3}}{4}{\left(\sqrt{x}-1\right)}^2=\frac{\sqrt{3}}{4}\left(x-2\sqrt{x}+1\right)$ .

Do đó, thể tích vật thể cần tính là:

$V=\underset{1}{\overset{4}{\int }}S\left(x\right)dx$$=\underset{1}{\overset{4}{\int }}\frac{\sqrt{3}}{4}\left(x-2\sqrt{x}+1\right)dx$

$=\frac{\sqrt{3}}{4}\left(\frac{x^2}{2}-\frac{4}{3}{x}^{\frac{3}{2}}+x\right){|}_1^4=\frac{7\sqrt{3}}{24}$

• Tính thể tích khối tròn xoay

Cho hàm số f(x) liên tục, không âm trên đoạn [a; b].

Khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay.

Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm x Î [a; b] được một hình tròn có bán kính f(x).

Thể tích của khối tròn xoay này là $V=\pi \underset{a}{\overset{b}{\int }}{f}^2\left(x\right)dx$ .

Ví dụ 4. Tính thể tích khối tròn xoay tạo thành khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = f(x) = e^x, trục hoành và hai đường thẳng x = 0, x = 3.

Hướng dẫn giải

Thể tích vật thể cần tính là:

$V=\pi \underset{0}{\overset{3}{\int }}{f}^2\left(x\right)dx$$=\pi \underset{0}{\overset{3}{\int }}{e}^{2x}dx$$=\frac{\pi }{2}{e}^{2x}{|}_0^3=\frac{\pi }{2}\left(e^6-1\right)$.

Bài tập Ứng dụng hình học của tích phân

Bài 1. Cho hình phẳng (H) giới hạn bởi các đường thẳng y = x²; y = 0; x = 2. Tính thể tích V của khối tròn xoay thu được khi quay (H) quanh trục Ox.

A. $V=\frac{8}{3}$ .

B. $V=\frac{32}{5}$ .

C. $V=\frac{8\pi }{3}$ .

D. $V=\frac{32\pi }{5}$ .

Hướng dẫn giải

Đáp án đúng là: D

Thể tích cần tính là $V=\pi \underset{0}{\overset{2}{\int }}{x}^{4}dx=\pi \frac{x^5}{5}{|}_0^2=\frac{32\pi }{5}$ .

Bài 2. Cho hàm số y = f(x) xác định và liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b được tính theo công thức

A. $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$ .

B. $S=\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ .

C. $S=-\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ .

D. $S=\underset{b}{\overset{a}{\int }}\left|f\left(x\right)\right|dx$ .

Hướng dẫn giải

Đáp án đúng là: A

Dựa vào định nghĩa, ta chọn đáp án A.

Bài 3. Tính diện tích hình phẳng giới hạn bởi các đường y = 2^x, y = 0, x = 0, x = 2.

Hướng dẫn giải

Diện tích cần tính là:

$S=\underset{0}{\overset{2}{\int }}\left(2^x\right)dx=\underset{0}{\overset{2}{\int }}{2}^{x}dx=\frac{2^x}{\ln 2}{|}_0^2=\frac{3}{\ln 2}$.

Bài 4. Cho hình phẳng D giới hạn bởi đường cong $y=\sqrt{2+\cos x}$ , trục hoành và các đường thẳng x = 0, $x=\frac{\pi }{2}$ . Tính thể tích khối tròn xoay tạo thành khi D quay quanh trục hoành.

Hướng dẫn giải

Thể tích cần tính là:

$V=\pi \underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(2+\cos x\right)dx$$=\pi \left(2x+\sin x\right){|}_0^{\frac{\pi }{2}}$$=\pi \left(\pi +1\right)$.

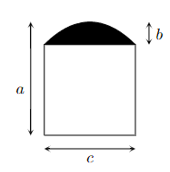
Bài 5. Nhà bạn Minh cần làm một cái cửa có dạng như hình vẽ bên dưới, nửa dưới là hình vuông, phần phía trên (phần tô đen) là một Parabol. Biết các kích thước a = 2,5m, b = 0,5m, c = 2m. Biết số tiền để làm 1 m² cửa là 1 triệu đồng. Tính số tiền để làm cửa.

Hướng dẫn giải

Chọn hệ trục tọa độ như hình vẽ

Gọi (P): y = ax² + bx + c là Parabol đi qua điểm A(1; 2) và có đỉnh là B(0; 2,5).

Khi đó ta có $\left\{\begin{array}{l}a+b+c=2\\ \frac{-b}{2a}=0\\ c=2,5\end{array}\right.$ $\iff \left\{\begin{array}{l}a=-0,5\\ b=0\\ c=2,5\end{array}\right.$ .

Vậy (P): y = −0,5x² + 2,5.

Do đó diện tích cửa là

$S=\underset{-1}{\overset{1}{\int }}\left(-0,5x^2+2,5\right)dx=\left(-\frac{1}{6}{x}^3+2,5x\right){|}_{-1}^1=\frac{7}{3}+\frac{7}{3}=\frac{14}{3}$  (m²).

Vậy số tiền cần làm cửa là $\frac{14}{3}$  triệu đồng.

Học tốt Ứng dụng hình học của tích phân

Các bài học để học tốt Ứng dụng hình học của tích phân Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 13: Ứng dụng hình học của tích phân