Tổng hợp lý thuyết Toán 12 Chương 4 - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Chương 4: Nguyên hàm và tích phân sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Tổng hợp lý thuyết Toán 12 Chương 4 - Kết nối tri thức

Lý thuyết tổng hợp Chương 4

1. Nguyên hàm

1.1 Nguyên hàm của một hàm số

• Khái niệm nguyên hàm

Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x thuộc K.

Chú ý. Trường hợp K = [a; b] thì các đẳng thức F'(a) = f(a) và F'(b) = f(b) được hiểu là đạo hàm bên phải tại điểm x = a và đạo hàm bên trái tại điểm x = b của hàm số F(x), tức là $\underset{x\to a^{+}}{\lim }\frac{F\left(x\right)-F\left(a\right)}{x-a}=f\left(a\right)$ và $\underset{x\to b^{-}}{\lim }\frac{F\left(x\right)-F\left(b\right)}{x-b}=f\left(b\right)$.

• Họ nguyên hàm của một hàm số

Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó:

a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K;

b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao cho G(x) = F(x) + C với mọi x $\in$ K.

Như vậy, nếu F(x) là một nguyên hàm của f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C (C là hằng số). Ta gọi F(x) + C (C $\in$ ℝ) là họ các nguyên hàm của f(x) trên K, kí hiệu bởi $\int f\left(x\right)dx$.

Chú ý

a) Để tìm họ các nguyên hàm (gọi tắt là tìm nguyên hàm) của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó $\int f\left(x\right)dx=F\left(x\right)+C,$ C là hằng số.

b) Người ta chứng minh được rằng, nếu hàm số f(x) liên tục trên khoảng K thì f(x) có nguyên hàm trên khoảng đó.

c) Biểu thức f(x)dx gọi là vi phân của nguyên hàm F(x), kí hiệu dF(x). Vậy dF(x) = F'(x)dx = f(x)dx.

d) Khi tìm nguyên hàm của một hàm số mà không chỉ rõ tập K, ta hiểu là tìm nguyên hàm của hàm số đó trên tập xác định của nó.

1.2. Tính chất cơ bản của nguyên hàm

• Nguyên hàm của tích một hàm số với một hằng số khác 0

$\int kf\left(x\right)dx=k\int f\left(x\right)dx\left(k\ne 0\right)$.

• Nguyên hàm của một tổng

$\int \left[f\left(x\right)+g\left(x\right)\right]dx=\int f\left(x\right)dx+\int g\left(x\right)dx$.

$\int \left[f\left(x\right)-g\left(x\right)\right]dx=\int f\left(x\right)dx-\int g\left(x\right)dx$.

1.3. Nguyên hàm của một số hàm số thường gặp

• Nguyên hàm của hàm số lũy thừa

+) Hàm số lũy thừa

Hàm số y = x^α, với α ∈ ℝ, được gọi là hàm số lũy thừa.

Tập xác định của hàm số lũy thừa y = x^α tùy thuộc vào giá trị của α. Cụ thể:

- Với α nguyên dương, tập xác định là ℝ.

- Với α nguyên âm hoặc bằng 0, tập xác định là ℝ\{0}.

- Với α không nguyên, tập xác định là (0; +∞).

+) Hàm số lũy thừa y = x^α (α $\in$ ℝ) có đạo hàm với mọi x > 0 và ${\left(x^{\alpha }\right)}^{\text{'}}=\alpha x^{\alpha -1}$.

+) Nguyên hàm của hàm số lũy thừa

$\int x^{\alpha }dx=\frac{x^{\alpha +1}}{\alpha +1}+C\left(\alpha \ne -1\right)$.

$\int \frac{1}{x}dx=\ln \left|x\right|+C$.

• Nguyên hàm của hàm số lượng giác

$\int \cos xdx=\sin x+C$;

$\int \sin xdx=-\cos x+C$;

$\int \frac{1}{{\cos }^{2}x}dx=\tan x+C$;

$\int \frac{1}{{\sin }^{2}x}dx=-\cot x+C$.

• Nguyên hàm của hàm số mũ

$\int e^{x}dx=e^x+C$.

$\int a^{x}dx=\frac{a^x}{\ln a}+C\left(0<a\ne 1\right)$.

2. Tích phân

2.1. Khái niệm tích phân

• Diện tích hình thang cong

+) Hình thang cong: Hình phẳng giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b, (a < b), trong đó f(x) là hàm liên tục không âm trên đọan [a; b], gọi là một hình thang cong.

+) Diện tích hình thang cong

Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b là S = F(b) – F(a), trong đó F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b].

• Định nghĩa tích phân

Cho f(x) là hàm số liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b] thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ .

Chú ý

a) Hiệu F(b) – F(a) thường được kí hiệu là $F\left(x\right)|\begin{array}{c}b\\ a\end{array}$ . Như vậy $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=F\left(x\right)|\begin{array}{c}b\\ a\end{array}$ .

b) Ta gọi $\underset{a}{\overset{b}{\int }}$ là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

c) Trong trường hợp a = b hoặc a > b, ta quy ước:

$\underset{a}{\overset{a}{\int }}f\left(x\right)dx=0;\underset{a}{\overset{b}{\int }}f\left(x\right)dx=-\underset{b}{\overset{a}{\int }}f\left(x\right)dx$ .

• Ý nghĩa hình học của tích phân

Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì tích phân $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$  là diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b. Vậy S = $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ .

2.2. Tính chất của tích phân

1) $\underset{a}{\overset{b}{\int }}kf\left(x\right)dx=k\underset{a}{\overset{b}{\int }}f\left(x\right)dx$  (k là hằng số);

2) $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx+\underset{a}{\overset{b}{\int }}g\left(x\right)dx$ ;

3) $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx-\underset{a}{\overset{b}{\int }}g\left(x\right)dx$ ;

4) $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{c}{\int }}f\left(x\right)dx+\underset{c}{\overset{b}{\int }}f\left(x\right)dx$  (a < c < b).

3. Ứng dụng hình học của tích phân

3.1. Ứng dụng tích phân để tính diện tích hình phẳng

• Hình phẳng giới hạn bởi một đồ thị hàm số, trục hoành và hai đường thẳng x = a, x = b.

Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số f(x) liên tục, trục hoành và hai đường thẳng x = a, x = b (a < b), được tính bằng công thức $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$ .

• Hình phẳng giới hạn bởi hai đồ thị hàm số và hai đường thẳng x = a, x = b

Diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a, x = b, được tính bằng công thức $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$ .

Chú ý: Nếu f(x) – g(x) không đổi dấu trên đoạn [a; b] thì

$S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx=\left|\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx\right|$

3.2. Ứng dụng tích phân để tính thể tích vật thể

• Tính thể tích vật thể

Cho một vật thể trong không gian Oxyz. Gọi ẞ là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ x = a, x = b. Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích là S(x). Giả sử S(x) là hàm liên tục trên đoạn [a; b]. Khi đó thể tích V của phần vật thể ẞ được tính bởi công thức $V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx$.

• Tính thể tích khối tròn xoay

Cho hàm số f(x) liên tục, không âm trên đoạn [a; b].

Khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay.

Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm x $\in$ [a; b] được một hình tròn có bán kính f(x).

Thể tích của khối tròn xoay này là $V=\pi \underset{a}{\overset{b}{\int }}{f}^2\left(x\right)dx$ .

Bài tập ôn tập Chương 4

1. Bài tập trắc nghiệm

Bài 1. Một nguyên hàm của hàm số f(x) = 9^x + 3x² là:

A. F(x) = 9^x + x³.

B. F(x) = 9^xln9 + x³.

C. $F\left(x\right)=\frac{9^x}{\ln 9}+6x$.

D. $F\left(x\right)=\frac{9^x}{\ln 9}+x^3$.

Hướng dẫn giải

Đáp án đúng là: D

Vì $F^{\text{'}}\left(x\right)={\left(\frac{9^x}{\ln 9}+x^3\right)}^{\text{'}}=9^x+3x^2$ nên $F\left(x\right)=\frac{9^x}{\ln 9}+x^3$là một nguyên hàm của hàm số f(x) = 9^x + 3x².

Bài 2. Các mệnh đề sau, mệnh đề nào sai?

A. $\int kf\left(x\right)dx=k\int f\left(x\right)dx,k\ne 0$.

B. $\int f\left(x\right).g\left(x\right)dx=\int f\left(x\right)dx.\int g\left(x\right)dx$.

C. $\int \left[f\left(x\right)+g\left(x\right)\right]dx=\int f\left(x\right)dx+\int g\left(x\right)dx$.

D. $\int \frac{1}{x}dx=\ln \left|x\right|+C$.

Hướng dẫn giải

Đáp án đúng là: B

Từ các tính chất của nguyên hàm, ta thấy đáp án B là sai.

Bài 3. Một nguyên hàm của hàm số f(x) = 9^x + 3x² là:

A. F(x) = 9^x + x³.

B. F(x) = 9^xln9 + x³.

C. $F\left(x\right)=\frac{9^x}{\ln 9}+6x$.

D. $F\left(x\right)=\frac{9^x}{\ln 9}+x^3$.

Hướng dẫn giải

Đáp án đúng là: D

Vì $F^{\text{'}}\left(x\right)={\left(\frac{9^x}{\ln 9}+x^3\right)}^{\text{'}}=9^x+3x^2$nên $F\left(x\right)=\frac{9^x}{\ln 9}+x^3$là một nguyên hàm của hàm số f(x) = 9^x + 3x².

Bài 4. Các mệnh đề sau, mệnh đề nào sai?

A. $\int kf\left(x\right)dx=k\int f\left(x\right)dx,k\ne 0$.

B. $\int f\left(x\right).g\left(x\right)dx=\int f\left(x\right)dx.\int g\left(x\right)dx$.

C. $\int \left[f\left(x\right)+g\left(x\right)\right]dx=\int f\left(x\right)dx+\int g\left(x\right)dx$.

D. $\int \frac{1}{x}dx=\ln \left|x\right|+C$.

Hướng dẫn giải

Đáp án đúng là: B

Từ các tính chất của nguyên hàm, ta thấy đáp án B là sai.

Bài 5. Biết $\underset{1}{\overset{5}{\int }}f\left(x\right)dx=4$ . Giá trị của $\underset{1}{\overset{5}{\int }}3f\left(x\right)dx$  bằng

A. 7.

B. $\frac{4}{3}$ .

C. 64.

D. 12.

Hướng dẫn giải

Đáp án đúng là: D

Ta có $\underset{1}{\overset{5}{\int }}3f\left(x\right)dx=3\underset{1}{\overset{5}{\int }}f\left(x\right)dx$  = 3.4 = 12.

Bài 6. Biết F(x) = x³ là một nguyên hàm của hàm số f(x) trên ℝ. Giá trị của $\underset{1}{\overset{2}{\int }}\left(2+f\left(x\right)\right)dx$  bằng

A. $\frac{23}{4}$ .

B. 7.

C. 9.

D. $\frac{15}{4}$ .

Hướng dẫn giải

Đáp án đúng là: C

Ta có $\underset{1}{\overset{2}{\int }}\left(2+f\left(x\right)\right)dx$$=\underset{1}{\overset{2}{\int }}2dx+\underset{1}{\overset{2}{\int }}f\left(x\right)dx$$=2x{|}_1^2+F\left(x\right){|}_1^2$

$=2+x^3{|}_1^2$  = 9.

2. Bài tập tự luận

Bài 1. Tìm

a) $\int \left(2x+e^x\right)dx$;

b) $\int \left(\sin x-\cos x\right)dx$.

Hướng dẫn giải

a) $\int \left(2x+e^x\right)dx$$=2\int xdx+\int e^{x}dx$$=2.\frac{x^2}{2}+e^x+C$

$=x^2+e^x+C$.

b) $\int \left(\sin x-\cos x\right)dx$$=\int \sin xdx-\int \cos xdx$

$=-\cos x-\sin x+C$ .

Bài 2. Tìm

a) $\int \frac{x^2+2\sqrt{x}+3}{x^3}dx$;                        b) $\int {10}^{2x}dx$;               c) $\int \frac{2^x-1}{e^x}dx$.

Hướng dẫn giải

a) $\int \frac{x^2+2\sqrt{x}+3}{x^3}dx$$=\int \frac{1}{x}dx+2\int x^{\frac{-5}{2}}dx+3\int x^{-3}dx$

$=\ln \left(x\right)-\frac{4}{3}{x}^{\frac{-3}{2}}-\frac{3}{2}{x}^{-2}+C$ .

b) $\int {10}^{2x}dx$$=\int {100}^{x}dx=\frac{{100}^x}{\ln 100}+C$ .

c) $\int \frac{2^x-1}{e^x}dx$$=\int \frac{2^x}{e^x}dx-\int \frac{1}{e^x}dx$$=\int {\left(\frac{2}{e}\right)}^{x}dx-\int {\left(\frac{1}{e}\right)}^{x}dx$

$=\frac{{\left(\frac{2}{e}\right)}^x}{\ln \frac{2}{e}}-\frac{{\left(\frac{1}{e}\right)}^x}{\ln \frac{1}{e}}+C$$=\frac{2^x}{e^x\left(\ln 2-1\right)}+\frac{1}{e^x}+C$.

Bài 3. Một vận động viên điền kinh chạy với gia tốc $a\left(t\right)=-\frac{1}{24}{t}^3+\frac{5}{16}{t}^2$(m/s²), trong đó t là khoảng thời gian tính từ lúc xuất phát. Hỏi vào thời điểm 5 (s) sau khi xuất phát thì vận tốc của vận động viên là bao nhiêu?

Hướng dẫn giải

Ta có $v\left(t\right)=\int a\left(t\right)dt=\int \left(-\frac{1}{24}{t}^3+\frac{5}{16}{t}^2\right)dt$

$=-\frac{1}{96}{t}^4+\frac{5}{48}{t}^3+C$

Vì v(0) = 0 nên C = 0.

Do đó $v\left(t\right)=-\frac{1}{96}{t}^4+\frac{5}{48}{t}^3$ .

Vào thời điểm 5 (s) sau khi xuất phát thì vận tốc của vận động viên là:

$v\left(5\right)=-\frac{1}{96}{.5}^4+\frac{5}{48}{.5}^3=\frac{625}{96}\approx 6,51$ (m/s).

Bài 4. Tính

a) $\underset{0}{\overset{1}{\int }}\left(3x+1\right)\left(x+3\right)dx$ ;                        b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^2\frac{x}{2}dx$ .

Hướng dẫn giải

a) $\underset{0}{\overset{1}{\int }}\left(3x+1\right)\left(x+3\right)dx$ $=\underset{0}{\overset{1}{\int }}\left(3x^2+10x+3\right)dx$

$=\left(x^3+5x^2+3x\right){|}_0^1$= 9.

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^2\frac{x}{2}dx$$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1+\cos x}{2}dx$$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1}{2}dx+\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{\cos x}{2}dx$

$=\frac{1}{2}\left(x+\sin x\right){|}_0^{\frac{\pi }{2}}$$=\frac{1}{2}\left(\frac{\pi }{2}+1\right)$

Bài 5. Tính $I=\underset{-2}{\overset{2}{\int }}\left|x^2-1\right|dx$ .

Hướng dẫn giải

$I=\underset{-2}{\overset{2}{\int }}\left|x^2-1\right|dx$$=\underset{-2}{\overset{-1}{\int }}\left|x^2-1\right|dx+\underset{-1}{\overset{1}{\int }}\left|x^2-1\right|dx+\underset{1}{\overset{2}{\int }}\left|x^2-1\right|dx$

$=\underset{-2}{\overset{-1}{\int }}\left(x^2-1\right)dx+\underset{-1}{\overset{1}{\int }}\left(1-x^2\right)dx+\underset{1}{\overset{2}{\int }}\left(x^2-1\right)dx$

$=\left(\frac{x^3}{3}-x\right){|}_{-2}^{-1}+\left(x-\frac{x^3}{3}\right){|}_{-1}^1+\left(\frac{x^3}{3}-x\right){|}_1^2$

$=\frac{2}{3}+\frac{2}{3}+\frac{2}{3}+\frac{2}{3}+\frac{2}{3}+\frac{2}{3}=4$

Bài 6. Cho hai quả bóng A, B di chuyển ngược chiều nhau va chạm với nhau. Sau va chạm mỗi quả bóng nảy ngược lại một đoạn thì dừng hẳn. Biết sau khi va chạm, quả bóng A nảy ngược lại với vận tốc v_A(t) = 8 – 2t (m/s) và quả bóng B nảy ngược lại với vận tốc v_B(t) = 12 – 4t (m/s). Tính khoảng cách giữa hai quả bóng sau khi đã dừng hẳn (giả sử hai quả bóng đều chuyển động thẳng).

Hướng dẫn giải

Thời gian quả bóng A chuyển động từ lúc va chạm đến khi dừng hẳn là

v_A(t) = 0 $\iff$ 8 – 2t = 0 $\iff$ t = 4 (s).

Quãng đường quả bóng A di chuyển là

$S_A=\underset{0}{\overset{4}{\int }}\left(8-2t\right)dt=\left(8t-t^2\right){|}_0^4=16$  (m).

Thời gian quả bóng B chuyển động từ lúc va chạm đến khi dừng hẳn là

v_B(t) = 0 $\iff$ 12 – 4t = 0 $\iff$ t = 3 (s).

Quãng đường quả bóng B đi được là

$S_B=\underset{0}{\overset{3}{\int }}\left(12-4t\right)dt=\left(12t-2t^2\right){|}_0^3=18$  (m).

Khoảng cách giữa hai quả bóng sau khi đã dừng hẳn là:

S = S_A + S_B = 16 + 18 = 34 (m).

Bài 7. Tính diện tích hình phẳng giới hạn bởi các đường y = 2^x, y = 0, x = 0, x = 2.

Hướng dẫn giải

Diện tích cần tính là:

$S=\underset{0}{\overset{2}{\int }}\left|2^x\right|dx=\underset{0}{\overset{2}{\int }}{2}^{x}dx=\frac{2^x}{\ln 2}{|}_0^2=\frac{3}{\ln 2}$.

Bài 8. Cho hình phẳng D giới hạn bởi đường cong $y=\sqrt{2+\cos x}$ , trục hoành và các đường thẳng x = 0, $x=\frac{\pi }{2}$ . Tính thể tích khối tròn xoay tạo thành khi D quay quanh trục hoành.

Hướng dẫn giải

Thể tích cần tính là:

$V=\pi \underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(2+\cos x\right)dx$$=\pi \left(2x+\sin x\right){|}_0^{\frac{\pi }{2}}$$=\pi \left(\pi +1\right)$.

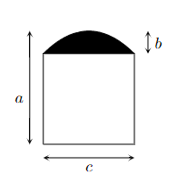
Bài 9. Nhà bạn Minh cần làm một cái cửa có dạng như hình vẽ bên dưới, nửa dưới là hình vuông, phần phía trên (phần tô đen) là một Parabol. Biết các kích thước a = 2,5m, b = 0,5m, c = 2m. Biết số tiền để làm 1 m² cửa là 1 triệu đồng. Tính số tiền để làm cửa.

Hướng dẫn giải

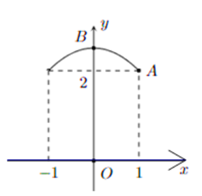
Chọn hệ trục tọa độ như hình vẽ

Gọi (P): y = ax² + bx + c là Parabol đi qua điểm A(1; 2) và có đỉnh là B(0; 2,5).

Khi đó ta có $\left\{\begin{array}{l}a+b+c=2\\ \frac{-b}{2a}=0\\ c=2,5\end{array}\right.$ $\iff \left\{\begin{array}{l}a=-0,5\\ b=0\\ c=2,5\end{array}\right.$ .

Vậy (P): y = −0,5x² + 2,5.

Do đó diện tích cửa là

$S=\underset{-1}{\overset{1}{\int }}\left(-0,5x^2+2,5\right)dx=\left(-\frac{1}{6}{x}^3+2,5x\right){|}_{-1}^1=\frac{7}{3}+\frac{7}{3}=\frac{14}{3}$  (m²).

Vậy số tiền cần làm cửa là $\frac{14}{3}$  triệu đồng.

Học tốt Toán 12 Chương 4

Các bài học để học tốt Bài tập cuối chương 4 Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài tập cuối chương 4