Lý thuyết Toán lớp 12 Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn - Kết nối tri thức

Lý thuyết Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

1. Tốc độ thay đổi của một đại lượng

Giả sử y là một hàm số của x và ta viết y = f(x). Nếu x thay đổi từ x₁ đến x₂ thì sự thay đổi của x là $∆$x = x₂ – x₁, và sự thay đổi tương ứng của y là $∆$y = f(x₂) – f(x₁).

- Tỉ số $\frac{\Delta y}{\Delta x}=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}$ được gọi là tốc độ thay đổi trung bình của y đối với x trên đoạn [x₁; x₂].

- Giới hạn$\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{x_2\to x_1}{\lim }\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}$ được gọi là tốc độ thay đổi tức thời của y đối với x tại điểm x = x₁.

Như vậy, đạo hàm f'(a) là tốc độ thay đổi tức thời của đại lượng y = f(x) đối với x tại điểm x = a. Dưới đây, chúng ta xem xét một số ứng dụng của ý tưởng này đối với vật lí, hóa học, sinh học và kinh tế:

• Nếu s = s(t) là hàm vị trí của một vật chuyển động trên một đường thẳng thì v = s'(t) biểu thị vận tốc tức thời của vật (tốc độ thay đổi của độ dịch chuyển theo thời gian). Tốc độ thay đổi tức thời của vận tốc theo thời gian là gia tốc tức thời của vật: a(t) = v'(t) = s"(t).

• Nếu C = C(t) là nồng độ của một chất tham gia phản ứng hóa học tại thời điểm t, thì C'(t) là tốc độ phản ứng tức thời (tức là độ thay đổi nồng độ) của chất đó tại thời điểm t.

• Nếu P = P(t) là số lượng cá thể trong một quần thể động vật hoặc thực vật tại thời điểm t thì P'(t) biểu thị tốc độ tăng trưởng tức thời của quần thể tại thời điểm t.

• Nếu C = C(x) là hàm chi phí, tức là tổng chi phí khi sản xuất x đơn vị hàng hóa, thì tốc độ thay đổi tức thời C'(x) của chi phí đối với số lượng đơn vị hàng được sản xuất được gọi là chi phí biên.

• Về ý nghĩa kinh tế, chi phí biên C'(x) xấp xỉ với chi phí để sản xuất thêm một đơn vị hàng hóa tiếp theo, tức là đơn vị hàng hóa thứ x + 1.

Ví dụ 1. Một chất điểm chuyển động có phương trình chuyển động là s(t) = −t³ + 6t² + 17t, với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Trong khoảng thời gian 8 giây đầu tiên, vận tốc của chất điểm đạt giá trị lớn nhất là bao nhiêu?

Hướng dẫn giải

Có v(t) = s'(t) = −3t² +12t + 17.

Bài toán trở thành tìm giá trị lớn nhất của v(t) = −3t² +12t + 17 trên [0; 8].

Có v'(t) = −6t + 12; v'(t) = 0 $\iff$ v = 2 (nhận).

Có v(0) = 17 m/s, v(2) = 29 m/s, v(8) = −79 m/s.

Do đó vận tốc chất điểm lớn nhất là 29 m/s khi t = 2 giây.

2. Một vài bài toán tối ưu đơn giản

• Quy trình giải một bài toán tối ưu hóa:

Bước 1: Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.

Bước 2: Chọn một đại lượng thích hợp nào đó, kí hiệu là x và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số Q = Q(x).

Bước 3: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số Q = Q(x) bằng các phương pháp đã biết và kết luận.

Ví dụ 2. Một lão nông chia đất cho con trai để người con canh tác riêng, biết người con sẽ được chọn miếng đất hình chữ nhật có chu vi bằng 800 m. Hỏi anh ta chọn mỗi kích thước của nó bằng bao nhiêu để diện tích canh tác lớn nhất?

Hướng dẫn giải

Gọi chiều dài miếng đất là x (m), (0 < x < 400).

Khi đó chiều rộng của miếng đất là 400 – x (m).

Diện tích của miếng đất là S(x) = x(400 – x) = 400x – x².

Bài toán trở thành tìm giá trị lớn nhất của S(x) = 400x – x² trên khoảng (0; 400).

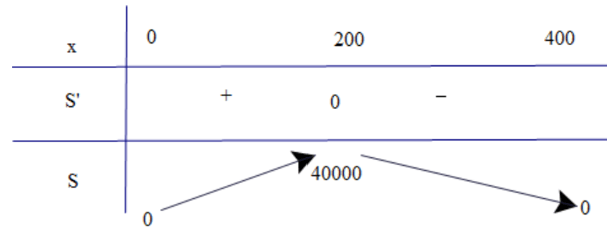
Có S'(x) = 400 – 2x; S'(x) = 0 $\iff$ x = 200.

Bảng biến thiên

- Hàm số đồng biến hay nghịch biến trên K còn được gọi chung là đơn điệu trên K. Việc tìm các khoảng đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của hàm số.

Dựa vào bảng biến thiên ta thấy $\underset{\left(0;400\right)}{\max }S=40000$ khi x = 200.

Vậy anh ta chọn miếng đất có kích thước hình vuông cạnh 200 m thì diện tích canh tác là lớn nhất.

• Hàm chi phí, hàm doanh thu, hàm lợi nhuận

- Nếu C(x) là hàm chi phí, tức là chi phí sản xuất x đơn vị của một sản phẩm nào đó thì chi phí biên là tốc độ thay đổi của C đối với x, tức là đạo hàm C'(x).

- Gọi p(x) là giá bán mỗi đơn vị mà công ty có thể tính nếu bán x đơn vị. Khi đó, p được gọi là hàm cầu (hay hàm giá) và chúng ta mong đợi đó là một hàm giảm của x. Nếu x đơn vị được bán và giá mỗi đơn vị là p(x) thì tổng doanh thu là R(x) = x.p(x) và R(x) được gọi là hàm doanh thu. Đạo hàm R'(x) của hàm doanh thu được gọi là hàm doanh thu biên và là tốc độ thay đổi của doanh thu đối với số lượng đơn vị sản phẩm bán ra.

- Nếu x đơn vị được bán thì tổng lợi nhuận là P(x) = R(x) – C(x) và P(x) được gọi là hàm lợi nhuận. Hàm lợi nhuận biên là đạo hàm P'(x) của hàm lợi nhuận.

Ví dụ 2. Công ty A chuyên sản xuất một loại sản phẩm và ước tính rằng với q sản phẩm được sản xuất thì tổng chi phí sẽ là C(q) = 3q² + 72q – 9789. Giá mỗi sản phẩm công ty sẽ bán với giá p(q) = 180 – 3q. Hãy xác định số sản phẩm công ty cần sản xuất sao cho công ty thu được lợi nhuận cao nhất.

Hướng dẫn giải

Gọi q (0 < q < 60) là số sản phẩm mà công ty A cần sản xuất để thu được lợi nhuận cao nhất.

Khi đó nếu bán hết số sản phẩm thì doanh thu sẽ là R(q) = q.(180 – 3q) = 180q – 3q².

Suy ra lợi nhuận mà công ty thu được là P(q) = R(q) – C(q) = −6q² + 108q + 9789.

Bài toán trở thành tìm giá trị lớn nhất của P(q) với 0 < q < 60.

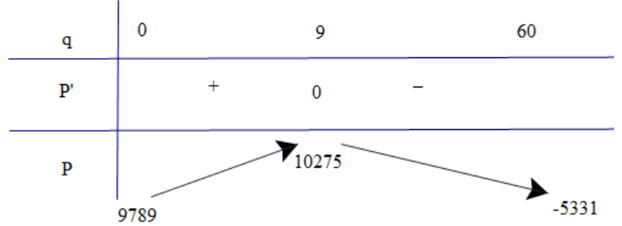
Có P'(q) = −12q + 108; P'(q) = 0 $\iff$ q = 9.

Bảng biến thiên

- Hàm số đồng biến hay nghịch biến trên K còn được gọi chung là đơn điệu trên K. Việc tìm các khoảng đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của hàm số.

Dựa vào bảng biến thiên ta có để lợi nhuận cao nhất thì công ty cần sản xuất 9 sản phẩm.

Bài tập Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

Bài 1. Một vật rơi tự do với phương trình chuyển động $S=\frac{1}{2}g{t}^2$, trong đó g = 9,8 m/s² và t tính bằng giây (s). Vận tốc của vật tại thời điểm t = 5s bằng

A. 49 m/s.                   

B. 25 m/s.                                    

C. 10 m/s.                                   

D. 18 m/s.

Hướng dẫn giải

Đáp án đúng là: A

Có v(t) = s'(t) = gt = 9,8t.

Khi đó v(5) = 9,8.5 = 49 m/s.

Bài 2. Chi phí xuất bản x cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, giấy in…) được cho bởi C(x) = 0,0001x² – 0,2x + 10000, C(x) được tính theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số $M\left(x\right)=\frac{T\left(x\right)}{x}$ với T(x) là tổng chi phí (xuất bản và phát hành) cho x cuốn tạp chí, được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản x cuốn. Khi chi phí trung bình cho mỗi cuốn tạp chí M(x) thấp nhất, tính chi phí cho mỗi cuốn tạp chí đó. Biết 1 vạn đồng = 10 000 đồng.

A. 20 000 đồng.

B. 15 000 đồng.

C. 10 000 đồng.

D. 22 000 đồng.

Hướng dẫn giải

Đáp án đúng là: D

Theo giả thiết ta có: T(x) = C(x) + 0,4x = 0,0001x² + 0,2x + 10000.

Có $M\left(x\right)=\frac{T\left(x\right)}{x}=\mathrm{0,0001}x+\frac{10000}{x}+\mathrm{0,2}\ge 2+\mathrm{0,2}=\mathrm{2,2}$ vạn đồng = 22000 đồng.

Dấu “=” xảy ra khi .

Bài 3. Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 000 000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê, mỗi căn hộ thêm 50 000 đồng một tháng thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt trong một tháng là bao nhiêu?

Hướng dẫn giải

Gọi x là số căn hộ bỏ trống (0 < x < 50).

Khi đó số tiền cho thuê một phòng là 2 000 000 + 50 000x (đồng).

Tổng số tiền cho thuê phòng 1 tháng là

f(x) = (2 000 000 + 50 000x).(50 – x) = −50 000x² + 500 000x + 100 000 000 đồng.

Bài toán trở thành tìm x ∈ (0; 50) để f(x) lớn nhất.

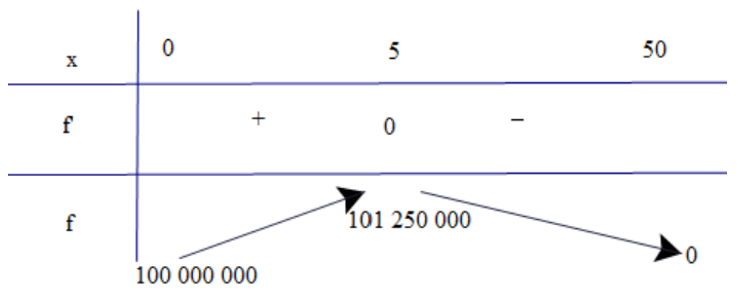
Có f'(x) = −100 000x + 500 000; f'(x) = 0 $\iff$ x = 5.

Bảng biến thiên

- Hàm số đồng biến hay nghịch biến trên K còn được gọi chung là đơn điệu trên K. Việc tìm các khoảng đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của hàm số.

Dựa vào bảng biến thiên, ta có doanh thu lớn nhất một tháng là 101 250 000 đồng khi có 5 phòng trống.

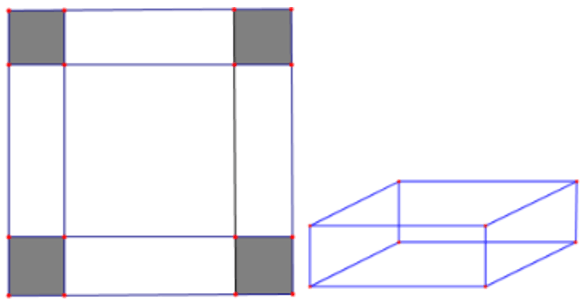
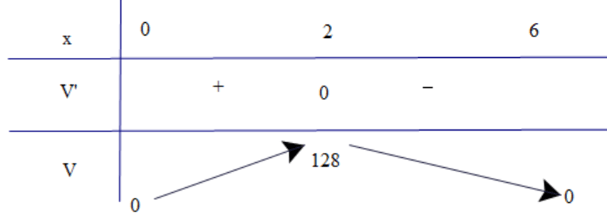
Bài 4. Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm, rồi gập tấm nhôm lại để được cái hộp không nắp (tham khảo hình vẽ bên). Tìm x để hộp nhận được có thể tích lớn nhất (giả thiết bề dày tấm nhôm không đáng kể).

- Hàm số đồng biến hay nghịch biến trên K còn được gọi chung là đơn điệu trên K. Việc tìm các khoảng đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của hàm số.

Hướng dẫn giải

Cái hộp không nắp có dạng hình hộp chữ nhật với đáy là hình vuông cạnh 12 – 2x (cm)  (0 < x < 6) và chiều cao là x (cm).

Khi đó thể tích V = (12 – 2x)².x = 4x³ – 48x² + 144x.

Bài toán trở thành tìm x ∈ (0; 6) để V lớn nhất.

Có V' = 12x² – 96x + 144; V' = 0 $\iff$ x = 2 (nhận) hoặc x = 6 (loại).

Bảng biến thiên

- Hàm số đồng biến hay nghịch biến trên K còn được gọi chung là đơn điệu trên K. Việc tìm các khoảng đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của hàm số.

Vậy x = 2 thì hộp có thể tích lớn nhất.

Bài 5. Một vật chuyển động theo quy luật $s=-\frac{1}{2}{t}^3+6t^2$ với t (giây) là khoảng thời gian từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian 6 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng bao nhiêu?

Hướng dẫn giải

Có v(t) = s'(t) = $-\frac{3}{2}{t}^2+12t=-\frac{3}{2}\left(t^2-8t+16\right)+24=-\frac{3}{2}{\left(t-4\right)}^2+24\le 24$.

Vậy vận tốc lớn nhất vật đạt được là 24 m/s khi t = 4 giây.

Học tốt Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

Các bài học để học tốt Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn