Lý thuyết Toán lớp 12 Phương trình đường thẳng trong không gian - Kết nối tri thức
Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 15: Phương trình đường thẳng trong không gian sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.
Lý thuyết Toán lớp 12 Phương trình đường thẳng trong không gian - Kết nối tri thức
Lý thuyết Phương trình đường thẳng trong không gian
1. Phương trình đường thẳng
• Vectơ chỉ phương của đường thẳng
Vectơ được gọi là vectơ chỉ phương của đường thẳng D nếu giá của song song hoặc trùng với .
Chú ý
+) Đường thẳng hoàn toàn xác định khi biết một điểm mà nó đi qua và một vectơ chỉ phương.
+) Nếu là một vectơ chỉ phương của thì (với k là một số khác 0) cũng là một vectơ chỉ phương của .
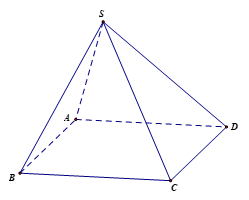
Ví dụ 1. Cho hình chóp S.ABCD, đáy là hình bình hành. Hãy chỉ ra các vectơ chỉ phương của đường thẳng BC mà điểm đầu và điểm cuối của vectơ đó đều là các đỉnh của hình chóp S.ABCD.
Hướng dẫn giải
Đường thẳng BC nhận là các vectơ chỉ phương của đường thẳng BC.
• Phương trình tham số của đường thẳng
Trong không gian Oxyz, cho đường thẳng đi qua điểm A(x0; y0; z0) và có vectơ chỉ phương . Hệ phương trình được gọi là phương trình tham số của đường thẳng (t là tham số, t ℝ).
Chú ý
+) Với các số a, b, c không đồng thời bằng 0, hệ phương trình xác định một đường thẳng đi qua điểm M(x0; y0; z0) và có vectơ chỉ phương .
+) Từ phương trình tham số của đường thẳng, mỗi giá trị của tham số tương ứng với một điểm thuộc đường thẳng và ngược lại.
Ví dụ 2. Viết phương trình tham số của đường thẳng đi qua điểm A(0; 1; 2) và có vectơ chỉ phương .
Hướng dẫn giải
Đường thẳng đi qua điểm A(0; 1; 2) và có vectơ chỉ phương có phương trình là: .
• Phương trình chính tắc của đường thẳng
Trong không gian Oxyz, cho đường thẳng đi qua điểm A(x0; y0; z0) và có vectơ chỉ phương với a, b, c là các số khác 0.
Hệ phương trình: được gọi là phương trình chính tắc của đường thẳng .
Ví dụ 3. Viết phương trình chính tắc của đường thẳng đi qua điểm A(−1; 1; 2) và có vectơ chỉ phương .
Hướng dẫn giải
Đường thẳng đi qua điểm A(−1; 1; 2) và có vectơ chỉ phương có phương trình chính tắc là: .
• Phương trình đường thẳng đi qua hai điểm
Trong không gian Oxyz, cho hai điểm phân biệt A1(x1; y1; z1) và A2(x2; y2; z2). Đường thẳng A1A2 có vectơ chỉ phương .
+) Đường thẳng A1A2 có phương trình tham số là: .
+) Trong trường hợp x1 ≠ x2, y1 ≠ y2, z1 ≠ z2 thì đường thẳng A1A2 có phương trình chính tắc là: .
Ví dụ 4. Lập phương trình tham số của đường thẳng đi qua hai điểm M(1; 1; 1) và N(1; −3; 2).
Hướng dẫn giải
Đường thẳng MN đi qua điểm M(1; 1; 1) nhận làm vectơ chỉ phương có phương trình tham số là: .
2. Hai đường thẳng vuông góc
Trong không gian Oxyz, cho hai đường thẳng 1, 2 tương ứng có vectơ chỉ phương , . Khi đó .
Ví dụ 5. Trong không gian Oxyz, cho hai đường thẳng:
d1: và d2: .
Chứng minh rằng hai đường thẳng trên vuông góc với nhau.
Hướng dẫn giải
Ta có ; .
Vì . Do đó d1 d2.
3. Vị trí tương đối giữa hai đường thẳng
Trong không gian Oxyz, cho hai đường thẳng , lần lượt đi qua các điểm A1(x1; y1; z1), A2(x2; y2; z2) và tương ứng có vectơ chỉ phương . Khi đó:
+) // cùng phương với và A1 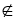
+) ≡ cùng phương với và A1 .
+) và cắt nhau
.
+) và chéo nhau .
Ví dụ 6. Trong không gian Oxyz, cho hai đường thẳng d1: và d2: . Xác định vị trí tương đối của hai đường thẳng trên.
Hướng dẫn giải
Đường thẳng d1 đi qua điểm A(1; 3; 0) và có vectơ chỉ phương .
Đường thẳng d2 đi qua điểm B(−2; 2; 3) và có vectơ chỉ phương .
Có và .
Vì .
Do đó d1 và d2 chéo nhau.
Chú ý. Để xét vị trí tương đối giữa hai đường thẳng, ta cũng có thể dựa vào các vectơ chỉ phương và phương trình của hai đường thẳng đó theo tiêu chuẩn sau đây.
Trong không gian Oxyz, cho hai đường thẳng 1, 2 tương ứng có vectơ chỉ phương và có phương trình tham số:
;
Xét hệ phương trình hai ẩn t, s: (*).
Khi đó:
+) 1 // 2 cùng phương với và hệ (*) vô nghiệm.
+) 1 ≡ 2 Hệ (*) có vô số nghiệm.
+) 1 cắt 2 Hệ (*) có nghiệm duy nhất.
+) 1 và 2 chéo nhau và không cùng phương và hệ (*) vô nghiệm.
Ví dụ 7. Trong không gian Oxyz, cho hai đường thẳng d1: và d2: . Xác định vị trí tương đối của hai đường thẳng trên.
Hướng dẫn giải
Xét hệ phương trình .
Do đó hệ có nghiệm duy nhất nên d1 và d2 cắt nhau.
Bài tập Phương trình đường thẳng trong không gian
Bài 1. Trong không gian Oxyz, cho đường thẳng d: . Vectơ nào dưới đây là một vectơ chỉ phương của d?
A. .
B. .
C. .
D. .
Hướng dẫn giải
Đáp án đúng là: B
Đường thẳng d: có một vectơ chỉ phương là .
Bài 2. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 1; 0) và B(0; 1; 2). Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng AB.
A. .
B. .
C. .
D. .
Hướng dẫn giải
Đáp án đúng là: C
Có . Do đó đường thẳng AB nhận làm một vectơ chỉ phương.
Bài 3. Viết phương trình tham số và phương trình chính tắc của đường thẳng trong các trường hợp sau:
a) đi qua điểm A(−1; −3; 4) và có vectơ chỉ phương .
b) đi qua điểm A(−2; 2; 1) và vuông góc với mặt phẳng (α): x + 2y – 3z + 4 = 0.
Hướng dẫn giải
a) Đường thẳng đi qua điểm A(−1; −3; 4) và có vectơ chỉ phương có phương trình tham số là và phương trình chính tắc là .
b) Có .
Vì (α) nên đường thẳng nhận làm một vectơ chỉ phương.
Đường thẳng đi qua điểm A(−2; 2; 1), có làm một vectơ pháp tuyến có phương trình tham số là và phương trình chính tắc là .
Bài 4. Cho hai đường thẳng d1: và d2: .
Chứng minh rằng d1 và d2 cắt nhau. Tìm tọa độ giao điểm của d1 và d2.
Hướng dẫn giải
Đường thẳng d2 có phương trình tham số là .
Xét hệ phương trình .
Hệ có nghiệm duy nhất. Do đó d1 và d2 cắt nhau.
Với t = 4 thay vào phương trình đường thẳng d1 ta có .
Vậy tọa độ giao điểm của hai đường thẳng là (10; −1; 0).
Bài 5. Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10; 3; 0) và chuyển động đều theo đường cáp có vectơ chỉ phương là . Viết phương trình chính tắc của đường cáp.
Hướng dẫn giải
Phương trình chính tắc của đường cáp là .
Học tốt Phương trình đường thẳng trong không gian
Các bài học để học tốt Phương trình đường thẳng trong không gian Toán lớp 12 hay khác: