Giải Toán 12 trang 48 Tập 1 Kết nối tri thức
Với Giải Toán 12 trang 48 Tập 1 trong Bài 6: Vectơ trong không gian Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 48.
Giải Toán 12 trang 48 Tập 1 Kết nối tri thức
Luyện tập 2 trang 48 Toán 12 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Trong ba vectơ và vectơ nào bằng vectơ ?
b) Gọi M là một điểm thuộc cạnh AD. Xác định điểm sao cho .
Lời giải:
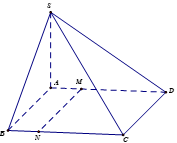
a) Vì ABCD là hình bình hành nên AB // CD và AB = CD.
Do đó hai vectơ và có cùng độ dài và cùng hướng nên hai vectơ đó bằng nhau.
Vì AB và SC chéo nhau nên hai vectơ và không cùng phương. Do đó hai vectơ và không bằng nhau.
Vì hai vectơ và không cùng phương nên hai vectơ và không bằng nhau.
b) Qua M vẽ đường thẳng song song với AB cắt BC tại N.
Tứ giác ABNM có AB // MN, AM // BN nên tứ giác ABNM là hình bình hành.
Do đó AB = MN.
Ta lại có AB // NM nên hai vectơ có cùng độ dài và cùng hướng.
Suy ra .
Vậy điểm N cần tìm là giao điểm của đường thẳng qua M song song với AB và cạnh BC.
Vận dụng 1 trang 48 Toán 12 Tập 1: Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lần tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển có bằng nhau không? Giải thích vì sao.
Lời giải:
Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 15 lên tầng 22 là .
Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 22 lên tầng 29 là .
Vì hai vectơ đều dịch chuyển từ tầng thấp nên tầng cao nên hai vectơ này cùng hướng.
Và .
Do đó ta có .
Vậy các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển bằng nhau.
Lời giải bài tập Toán 12 Bài 6: Vectơ trong không gian hay khác:

