Giải Toán 12 trang 58 Tập 1 Kết nối tri thức

❮ Bài trước Bài sau ❯

Với Giải Toán 12 trang 58 Tập 1 trong Bài 6: Vectơ trong không gian Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 58.

Giải Toán 12 trang 58 Tập 1 Kết nối tri thức

Bài 2.1 trang 58 Toán 12 Tập 1: Trong không gian, cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ phân biệt và đều khác $\vec{0}$ . Những mệnh đề nào sau đây là đúng?

a) Nếu $\vec{a}$ và $\vec{b}$ đều cùng hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng.

b) Nếu $\vec{a}$ và $\vec{b}$ đều ngược hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng.

c) Nếu $\vec{a}$ và $\vec{b}$ đều cùng hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ ngược hướng.

d) Nếu $\vec{a}$ và $\vec{b}$ đều ngược hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ ngược hướng.

Lời giải:

Các câu đúng là:

a) Nếu $\vec{a}$ và $\vec{b}$ đều cùng hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng.

b) Nếu $\vec{a}$ và $\vec{b}$ đều ngược hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng.

Bài 2.2 trang 58 Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2, AD = 3 và AA' = 4. Tính độ dài của các vectơ $\vec{B B^{'}}, \vec{B D}$ và $\vec{B D^{'}}$ .

Lời giải:

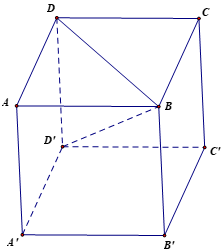
Bài 2.2 trang 58 Toán 12 Kết nối tri thức Tập 1

Vì ABCD.A'B'C'D' là hình hộp chữ nhật nên AA' = BB' = DD' = 4. Suy ra $|\vec{B B^{'}}| = 4.$

Xét DABD vuông tại A, có $B D = \sqrt{A B^{2} + A D^{2}} = \sqrt{4 + 9} = \sqrt{13}$ .

Suy ra $|\vec{B D}| = \sqrt{13}$ .

Xét DDD'B vuông tại D, có $B D^{'} = \sqrt{D B^{2} + D {D^{'}}^{2}} = \sqrt{13 + 16} = \sqrt{29}$ .

Suy ra $|\vec{B D^{'}}| = \sqrt{29}$ .

Bài 2.3 trang 58 Toán 12 Tập 1: Một chiếc bàn cân đối hình chữ nhật được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và bốn chân bàn vuông góc với mặt sàn như Hình 2.29. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ $\vec{a}$ ) phân tán đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ ).

a) Hãy chỉ ra mối quan hệ về phương và hướng của các vectơ $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ và $\vec{e}$ .

b) Giải thích vì sao các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ đôi một bằng nhau.

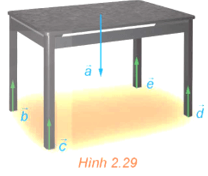
Bài 2.3 trang 58 Toán 12 Kết nối tri thức Tập 1

Lời giải:

a) Các vectơ $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ và $\vec{e}$ đều cùng phương với nhau.

Các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ đều ngược hướng với $\vec{a}$ nên các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ cùng hướng với nhau.

b) Do trọng lực phân tán đều qua các chân bàn nên các phản lực có độ lớn như nhau.

Suy ra các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ có độ dài bằng nhau hơn nữa $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ cùng hướng với nhau nên các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ đôi một bằng nhau.

Bài 2.4 trang 58 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:

a) $\vec{A B} + \vec{D D^{'}} + \vec{C^{'} D^{'}} = \vec{C C^{'}}$ ;

b) $\vec{A B} + \vec{C D^{'}} - \vec{C C^{'}} = \vec{0}$ ;

c) $\vec{B C} - \vec{C C^{'}} + \vec{D C} = \vec{A^{'} C}$ .

Lời giải:

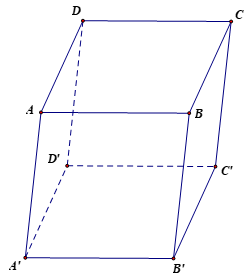
Bài 2.4 trang 58 Toán 12 Kết nối tri thức Tập 1

a) $\vec{A B} + \vec{D D^{'}} + \vec{C^{'} D^{'}} = \vec{C C^{'}}$

Vì ABCD.A'B'C'D' là hình hộp nên các mặt là hình bình hành

Nên $\vec{A B} = \vec{D C}; \vec{C^{'} D^{'}} = \vec{C D}$ .

Do đó $\vec{A B} + \vec{D D^{'}} + \vec{C^{'} D^{'}} = \vec{D C} + \vec{D D^{'}} + \vec{C D} = (\vec{D C} + \vec{C D}) + \vec{D D^{'}} = \vec{D D^{'}} = \vec{C C^{'}}$ .

b) $\vec{A B} + \vec{C D^{'}} - \vec{C C^{'}} = \vec{0}$

Vì $\vec{A B} = \vec{D C}$ nên $\vec{D C} + \vec{C D^{'}} - \vec{C C^{'}} = \vec{D D^{'}} - \vec{D D^{'}} = \vec{0}$ .

c) $\vec{B C} - \vec{C C^{'}} + \vec{D C} = \vec{A^{'} C}$

Ta có $\vec{B C} - \vec{C C^{'}} + \vec{D C} = - (\vec{C B} + \vec{C C^{'}} + \vec{C D}) = - \vec{C A^{'}} = \vec{A^{'} C}$ (quy tắc hình hộp).

Bài 2.5 trang 58 Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C' có $\vec{A A^{'}} = \vec{a}, \vec{A B} = \vec{b}$ và $\vec{A C} = \vec{c}$ . Hãy biểu diễn các vectơ sau qua các vectơ $\vec{a}, \vec{b}, \vec{c}$ :

a) $\vec{A B^{'}}$ ; b) $\vec{B^{'} C}$ ; c) $\vec{B C^{'}}$ .

Lời giải:

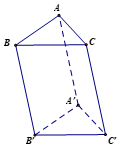
Bài 2.5 trang 58 Toán 12 Kết nối tri thức Tập 1

a) Vì ABB'A' là hình bình hành nên $\vec{A A^{'}} = \vec{B B^{'}}$ .

$\vec{A B^{'}}$ $= \vec{A B} + \vec{B B^{'}} = \vec{b} + \vec{a}$ .

b) $\vec{B^{'} C} = \vec{B^{'} B} + \vec{B C} = - \vec{B B^{'}} + \vec{B A} + \vec{A C} = - \vec{B B^{'}} - \vec{A B} + \vec{A C} = - \vec{a} - \vec{b} + \vec{c} .$

c) $\vec{B C^{'}} = \vec{B C} + \vec{C C^{'}} = \vec{A C} - \vec{A B} + \vec{A A^{'}} = \vec{c} - \vec{b} + \vec{a}$ .

Bài 2.6 trang 58 Toán 12 Tập 1: Cho hình chóp tứ giác S.ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành nếu và chỉ nếu $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ .

Lời giải:

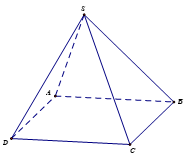
Bài 2.6 trang 58 Toán 12 Kết nối tri thức Tập 1

Chứng minh: Nếu ABCD là hình bình hành thì $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ .

Vì ABCD là hình bình hành nên

$\vec{A D} = \vec{B C}$ $\Leftrightarrow \vec{S D} - \vec{S A} = \vec{S C} - \vec{S B}$ $\Leftrightarrow \vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ .

Chứng minh: Nếu $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ thì ABCD là hình bình hành.

Có $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ $\Leftrightarrow \vec{S A} - \vec{S D} = \vec{S B} - \vec{S C}$ $\Leftrightarrow \vec{D A} = \vec{C B}$ .

Suy ra ABCD là hình bình hành.

Bài 2.7 trang 58 Toán 12 Tập 1: Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho SM = 2AM. Trên cạnh BC, lấy điểm N sao cho CN = 2BN. Chứng minh rằng $\vec{M N} = \frac{1}{3} (\vec{S A} + \vec{B C}) + \vec{A B}$ .

Lời giải:

Ta có $\vec{M N} = \vec{M A} + \vec{A B} + \vec{B N}$ (1).

Vì SM = 2AM nên $\vec{M A} = \frac{1}{3} \vec{S A}$ ; CN = 2BN nên $\vec{B N} = \frac{1}{3} \vec{B C}$ (2).

Từ (1), (2), ta có $\vec{M N} = \frac{1}{3} (\vec{S A} + \vec{B C}) + \vec{A B}$ .

Bài 2.8 trang 58 Toán 12 Tập 1: Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn $\vec{A I} = 3 \vec{I G}$ , ở đó G là trọng tâm của tam giác BCD. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm (H.2.30).

Bài 2.8 trang 58 Toán 12 Kết nối tri thức Tập 1

Lời giải:

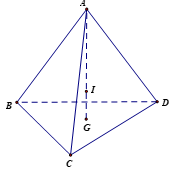
Giả sử khối rubik (đồng chất) hình tứ diện đều được mô phỏng như hình vẽ.

G là trọng tâm DBCD, I là trọng tâm của tứ diện

Vì ABCD là hình tứ diện đều nên AG $⊥$ (BCD) và AG = 8 cm.

Vì $\vec{A I} = 3 \vec{I G}$ nên 3 điểm A, I, G thẳng hàng và $I G = \frac{1}{4} A G$ .

Do đó IG $⊥$ (BCD). Khi đó $d (I, (B C D)) = I G = \frac{1}{4} A G = 2$ cm.

Lời giải bài tập Toán 12 Bài 6: Vectơ trong không gian hay khác:

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯