Giải Toán 12 trang 52 Tập 1 Kết nối tri thức

❮ Bài trước Bài sau ❯

Với Giải Toán 12 trang 52 Tập 1 trong Bài 6: Vectơ trong không gian Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 52.

Giải Toán 12 trang 52 Tập 1 Kết nối tri thức

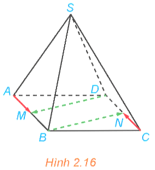
Luyện tập 6 trang 52 Toán 12 Tập 1: Trong Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, CD (H.2.16). Chứng minh rằng:

a) $\vec{B N}$ và $\vec{D M}$ là hai vectơ đối nhau;

b) $\vec{S D} - \vec{B N} - \vec{C M} = \vec{S C}$ .

Luyện tập 6 trang 52 Toán 12 Kết nối tri thức Tập 1

Lời giải:

a) Vì BMDN là hình bình hành nên BN // DM và BN = DM.

Hai vectơ $\vec{B N}$ và $\vec{D M}$ cùng phương, ngược hướng và có cùng độ dài nên là hai vectơ đối nhau.

b) Theo câu a, ta có: $\vec{D M} = - \vec{B N}$

Ta có $\vec{S D} - \vec{B N} - \vec{C M} = \vec{S D} + \vec{D M} - \vec{C M} = \vec{S M} + \vec{M C} = \vec{S C}$ .

Vận dụng 2 trang 52 Toán 12 Tập 1: Thang cuốn tại các trung tâm thương mại, siêu thị lớn hay nhà ga, sân bay thường có hai làn, trong đó có một làn lên và một làn xuống. Khi thang cuốn chuyển động, vectơ biểu diễn vận tốc của mỗi làn có là hai vectơ đối nhau hay không? Giải thích vì sao.

Vận dụng 2 trang 52 Toán 12 Kết nối tri thức Tập 1

Lời giải:

Quan sát thấy hai vectơ vận tốc cùng phương (vì làn lên và làn xuống song song) và ngược hướng (một làn đi lên và một làn đi xuống). Thông thường thì làn lên và làn xuống có cùng tốc độ di chuyển nên độ lớn của hai vectơ vận tốc bằng nhau. Vì vậy hai vectơ vận tốc là hai vectơ đối nhau.

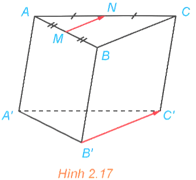
HĐ6 trang 52 Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của AB, AC (H.2.17).

a) Hai vectơ $\vec{M N}$ và $\vec{B^{'} C^{'}}$ có cùng phương không? Có cùng hướng không?

b) Giải thích vì sao $|\vec{M N}| = \frac{1}{2} |\vec{B^{'} C^{'}}|$ .

HĐ6 trang 52 Toán 12 Kết nối tri thức Tập 1

Lời giải:

a) Vì MN là đường trung bình của tam giác ABC nên MN // BC.

Tứ giác BCC'B' là hình bình hành nên BC // B'C'. Suy ra MN // B'C'.

Do đó hai vectơ $\vec{M N}$ và $\vec{B^{'} C^{'}}$ có cùng phương, cùng hướng.

b) Vì MN là đường trung bình của tam giác ABC nên $M N = \frac{1}{2} B C$ .

Tứ giác BCC'B' là hình bình hành nên BC = B'C'.

Do đó $M N = \frac{1}{2} B^{'} C^{'} .$

Suy ra $|\vec{M N}| = \frac{1}{2} |\vec{B^{'} C^{'}}|$ .

Lời giải bài tập Toán 12 Bài 6: Vectơ trong không gian hay khác:

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯