Cho tam giác ABC có trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB
Câu hỏi:
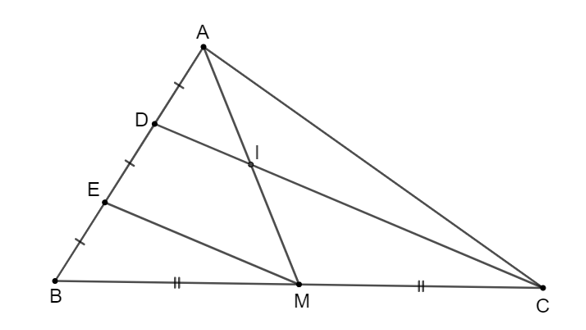
Cho tam giác ABC có trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.
a) Chứng minh DC // EM.
Trả lời:
a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.
Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.
Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.
Do đó DC // EM (tính chất đường trung bình).
Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết:
Câu 1:
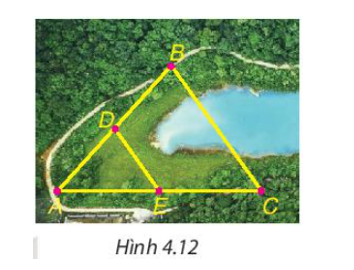
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
Xem lời giải »
Câu 2:
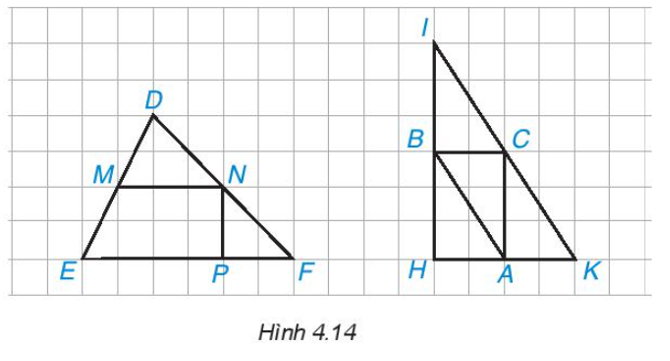
Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
Xem lời giải »
Câu 3:
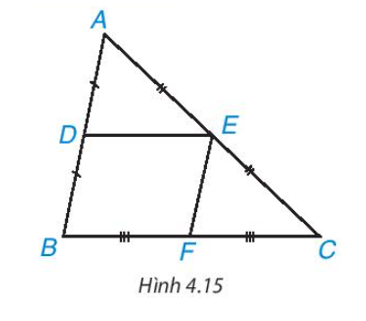
Cho DE là đường trung bình của tam giác ABC (H.4.15
Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.
Xem lời giải »
Câu 4:
Cho DE là đường trung bình của tam giác ABC (H.4.15
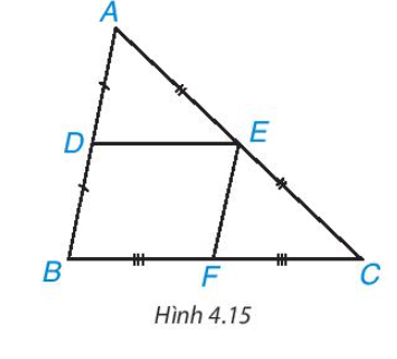
Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra .
Xem lời giải »
Câu 5:
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM.
Xem lời giải »
Câu 6:
Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật.
Xem lời giải »