Giải Toán 8 trang 87 Tập 2 Kết nối tri thức

Với Giải Toán 8 trang 87 Tập 2 trong Bài 34: Ba trường hợp đồng dạng của hai tam giác Toán 8 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 87.

Giải Toán 8 trang 87 Tập 2 Kết nối tri thức

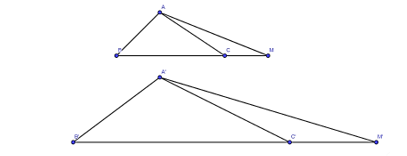
Luyện tập 2 trang 87 Toán 8 Tập 2: Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho $\frac{MC}{MB}=\frac{M\text{'}C\text{'}}{M\text{'}B\text{'}}$. Chứng minh rằng  ΔA'B'M' ∽ ΔABM.

Lời giải:

Có $\frac{MC}{MB}=\frac{M\text{'}C\text{'}}{M\text{'}B\text{'}}$ . Suy ra $\frac{MB-BC}{MB}=\frac{M\text{'}B\text{'}-B\text{'}C\text{'}}{M\text{'}B\text{'}}$

Suy ra $1-\frac{BC}{MB}=1-\frac{B\text{'}C\text{'}}{M\text{'}B\text{'}}$ . Do đó, $\frac{BC}{MB}=\frac{B\text{'}C\text{'}}{M\text{'}B\text{'}}$, suy ra $\frac{B\text{'}C\text{'}}{BC}=\frac{M\text{'}B\text{'}}{MB}$. (1)

Vì ΔA′B′C′ ∽ ΔABC. Suy ra $\widehat{B}=\widehat{B\text{'}}$ và $\frac{A\text{'}B\text{'}}{AB}=\frac{B\text{'}C\text{'}}{BC}$. (2)

Từ (1) và (2) suy ra $\frac{M\text{'}B\text{'}}{MB}=\frac{A\text{'}B\text{'}}{AB}$.

Xét tam giác ABM và tam giác A'B'M' có:

 $\frac{M\text{'}B\text{'}}{MB}=\frac{A\text{'}B\text{'}}{AB}$ và $\widehat{B}=\widehat{B\text{'}}$ (chứng minh trên).

Do đó ΔABM ∽ ΔA′B′M′ (c.g.c).

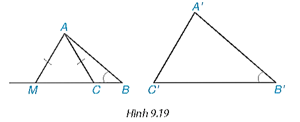
Tranh luận trang 87 Toán 8 Tập 2: Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A'B'C' có $\frac{A\text{'}B\text{'}}{AB}=\frac{A\text{'}C\text{'}}{AC}$ và $\widehat{B}=\widehat{B\text{'}}$ thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao?

Gợi ý: Khi góc ACB tù, lấy điểm M trên tia BC sao cho tam giác AMC cân (H.9.19) rồi xét xem trong hai tam giác ABC và ABM, tam giác nào đồng dạng với tam giác A'B'C'.

Lời giải:

Bạn Lan nhận xét không đúng.

Ví dụ lấy ∆ABM ∽ ∆A'B'C' với $\widehat{C\text{'}}=\widehat{M}<90°$ và lấy C trên đoạn MB sao cho ∆AMC cân tại A như H.9.19 thì ∆ABC và ∆A'B'C' không đồng dạng.

Lời giải bài tập Toán 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác Kết nối tri thức hay khác:

• Giải Toán 8 trang 83
• Giải Toán 8 trang 85
• Giải Toán 8 trang 88
• Giải Toán 8 trang 89
• Giải Toán 8 trang 90