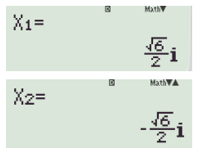Tổng hợp lý thuyết Toán 9 Chương 6 - Chân trời sáng tạo

---

Haylamdo biên soạn tổng hợp lý thuyết Toán 9 Chương 6: Hàm số y = ax (a ≠ 0) và Phương trình bậc hai một ẩn sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm Toán 9 Chương 6.

Tổng hợp lý thuyết Toán 9 Chương 6 - Chân trời sáng tạo

Tổng hợp lý thuyết Toán 9 Chương 6

1. Hàm số y = ax² (a ≠ 0)

– Hàm số y = ax² (a ≠ 0) xác định với mọi giá trị $x\in ℝ$ nên tập xác định của hàm số là $D=ℝ$.

2. Bảng giá trị của hàm số y = ax² (a ≠ 0)

Để lập bảng giá trị của hàm số y = ax² (a ≠ 0), ta lần lượt cho x nhận các giá trị x₁, x₂, x₃,... (x₁, x₂, x₃,... tăng dần) và tính các giá trị tương ứng của y rồi ghi vào bảng như sau:

3. Đồ thị của hàm số y = ax² (a ≠ 0)

Đồ thị của hàm số số y = ax² (a ≠ 0) là một đường cong đi qua gốc toạ độ, nhận trục tung làm trục đối xứng. Đường cong đó được gọi là một parabol đỉnh O.

• Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.

• Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.

Chú ý: Để vẽ đồ thị hàm số y = ax² (a ≠ 0), ta thực hiện các bước sau:

– Lập bảng giá trị của hàm số với một số giá trị của x (thường lấy 5 giá trị gồm 0 và hai cặp giá trị đối nhau).

– Trên mặt phẳng tọa độ Oxy, đánh dấu các điểm (x; y) trong bảng giá trị (gồm điểm (0; 0) và hai cặp điểm đối xứng nhau qua trục Oy).

– Vẽ đường parabol đi qua các điểm vừa được đánh dấu.

Vì đồ thị của hàm số y = ax² (a ≠ 0) luôn đi qua gốc toạ độ O và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị hàm số, ta chỉ cần tìm một số điểm bên phái trục Oy rồi lấy các điểm đối xứng với chúng qua trục Oy.

4. Phương trình bậc hai một ẩn

– Phương trình bậc hai một ẩn (còn gọi là phương trình bậc hai) là phương trình có dạng ax² + bx + c = 0, trong đó x là ẩn, a, b, c là những số cho trước gọi là các hệ số và a ≠ 0.

5. Giải một số phương trình bậc hai dạng đặc biệt

– Để giải các phương trình bậc hai có dạng ax² + bx = 0 hoặc ax² + c = 0 (với a ≠ 0, c < 0), ta có thể đưa phương trình về dạng phương trình tích rồi giải phương trình.

6. Công thức nghiệm của phương trình bậc hai

Cho phương trình ax² + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b² – 4ac.

• Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt:

                  $x_1=\frac{-b+\sqrt{\Delta }}{2a};x_2=\frac{-b-\sqrt{\Delta }}{2a}$.

• Nếu ∆ = 0 thì phương trình có nghiệm kép $x_1=x_2=\frac{-b}{2a}$.

• Nếu ∆ < 0 thì phương trình vô nghiệm.

7. Tìm nghiệm của phương trình bậc hai một ẩn bằng máy tính cầm tay

– Ta có thể sử dụng máy tính cầm tay để tìm nghiệm của các phương trình bậc hai bằng cách thực hiện các bước sau:

• Ấn nút ON để khởi động máy.

•  Ấn nút MODE.

• Ấn nút 5

• Ấn nút 3, nhập các hệ số a, b, c

• Ấn nút = để xem các nghiệm của phương trình.

Chú ý: Nếu các nghiệm của phương trình được hiển thị dưới dạng ai (trong đó a là hệ số như dưới đây) thì phương trình vô nghiệm.

8. Giải bài toán bằng cách lập phương trình bậc hai

Để giải bài toán bằng cách lập phương trình bậc hai, ta thực hiện như sau:

• Bước 1: Lập phương trình:

– Chọn ẩn và đặt điều kiện thích hợp cho ẩn.

– Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

– Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

• Bước 2: Giải phương trình nói trên.

• Bước 3: Kiểm tra các nghiệm tìm được ở Bước 2 có thoả mãn điều kiện của ẩn hay không, rồi trả lời bài toán.

9. Định lý Viète

Nếu phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thì tổng và tích của hai nghiệm đó là:

                                                   $S=x_1+x_2=-\frac{b}{a}$;

                                                   $P=x_1.x_2=\frac{c}{a}$.

Nhận xét:

– Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x₁ = 1, nghiệm còn lại là $x_2=\frac{c}{a}$.

– Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a – b + c = 0 thì phương trình có một nghiệm là x₁ = –1, nghiệm còn lại là $x_2=-\frac{c}{a}$.

10. Tìm hai số khi biết tổng và tích của chúng

Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình:

x² – Sx + P = 0.

Điều kiện để có hai số đó là S² – 4P ≥ 0.

Bài tập ôn tập Chương 6

Bài 1. Trong các hàm số sau, đồ thị hàm số nào nằm dưới trục hoành?

A. y = x².

B. y = 2x².

C. $y=\frac{1}{2}{x}^2$.

D. y = –x².

Hướng dẫn giải:

Đáp án đúng là: D

Đồ thị hàm số y = –x² nằm dưới trục hoành vì a = –1 < 0.

Bài 2. Điểm cao nhất của đồ thị của hàm số số y = ax² (a < 0) có hoành độ là

A. –1.

B. 0.

C. 1.

D. 2.

Hướng dẫn giải:

Đáp án đúng là: B

Khi a < 0 thì đồ thị của hàm số số y = ax² nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị. Tọa độ của điểm O là (0; 0).

Bài 3. Số nghiệm của phương trình 3x² + 5x – 6 = 0 là

A. 1.

B. 2.

C. Vô nghiệm.

D. Một đáp án khác.

Hướng dẫn giải

Đáp án đúng là: B.

Ta có: ∆ = 5² – 4 . 3 . (–6) = 97 > 0 nên phương trình có 2 nghiệm phân biệt.

Bài 4. Nghiệm dương của phương trình x² + 5x – 6 = 0 là

A. 6.

B. 3.

C. 1.

D. Phương trình không có nghiệm dương.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: ∆ = 5² – 4 . 1 . (–6) = 49 > 0 nên phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-5+\sqrt{49}}{2.1}=1$;

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-5-\sqrt{49}}{2.1}=-6.$

Vậy nghiệm dương của phương trình là x = 1.

Bài 5. Tổng và tích của hai nghiệm của phương trình 5x² + 7x – 3 = 0 là

A. $\frac{7}{5}$ và $\frac{3}{5}.$

B. $\frac{7}{5}$ và $-\frac{3}{5}$.

C. $-\frac{7}{5}$ và $\frac{3}{5}.$

D. $-\frac{7}{5}$ và $-\frac{3}{5}$.

Hướng dẫn giải

Đáp án đúng là: D

Áp dụng định lý Viète, ta có: $S=x_1+x_2=-\frac{b}{a}=-\frac{7}{5}$;

                                              $P=x_1.x_2=\frac{c}{a}=-\frac{3}{5}$.

Bài 6. Giả sử x₁, x₂ là hai nghiệm của phương trình x² – 5x + 3 = 0. Giá trị của biểu thức x₁² + x₂² là

A. 16.

B. 17.

C. 18.

D. 19.

Hướng dẫn giải

Đáp án đúng là: D

Áp dụng hệ thức Viète, ta có:

$S=x_1+x_2=-\frac{b}{a}=-\frac{-5}{1}=5;$

$P=x_1.x_2=\frac{c}{a}=-\frac{3}{1}=-3.$

x₁² + x₂² = (x₁ + x₂)² – 2x₁x₂ = 5² – 2.(–3) = 19.

Bài 7. Lập bảng giá trị của hàm số $y=\frac{1}{3}{x}^2$ với các giá trị x lần lượt bằng –2; –1; 2; 5; 8

Hướng dẫn giải

Bảng giá trị của hàm số $y=\frac{1}{3}{x}^2$:

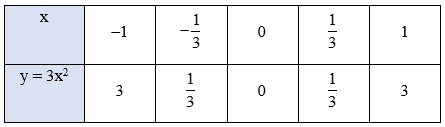
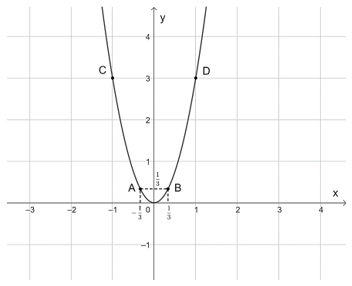
Bài 8. Vẽ đồ thị của hàm số y = 3x².

Hướng dẫn giải

Bảng giá trị của hàm số:

Trên mặt phẳng tọa độ Oxy, lấy các điểm $A\left(-\frac{1}{3};\frac{1}{3}\right)$; $B\left(\frac{1}{3};\frac{1}{3}\right)$; O(0; 0); C(–1; 3); D(1; 3).

Đồ thị của hàm số y = 3x² là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như sau:

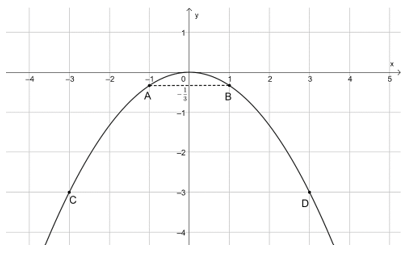
Bài 9. Vẽ đồ thị của hàm số $y=-\frac{1}{3}{x}^2$.

Hướng dẫn giải

Bảng giá trị của hàm số:

Trên mặt phẳng tọa độ Oxy, lấy các điểm $A\left(-1;-\frac{1}{3}\right)$; $B\left(1;-\frac{1}{3}\right)$; O(0; 0); C(–3; –3); D(3; –3).

Đồ thị của hàm số $y=-\frac{1}{3}{x}^2$ là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như sau:

Bài 10. Viết công thức tính diện tích của hình vuông cạnh 2a. Lập bảng giá trị diện tích của hình lập phương với các giá trị a lần lượt là 1; 2; 3.

Hướng dẫn giải

Diện tích hình vuông là $S={\left(2a\right)}^2=4a^2$.

Bảng giá trị của hàm số:

Bài 11. Giải các phương trình sau:

a) x² – x – 11 = 0;

b) –2x² + x – 3 = 0.

Hướng dẫn giải

a) Ta có: ∆ = (–1)² – 4 . 1 . (–11) = 45 > 0 nên phương trình có 2 nghiệm phân biệt.

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-\left(-1\right)+\sqrt{45}}{2.1}=\frac{1+3\sqrt{5}}{2}$;

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-\left(-1\right)-\sqrt{45}}{2.1}=\frac{1-3\sqrt{5}}{2}.$

b) Ta có: ∆ = 1² – 4 . (–2) . (–3) = –23 < 0 nên phương trình vô nghiệm.

Bài 12. Một mảnh đất hình chữ nhật có chu vi bằng 28 m. Đường chéo của hình chữ nhật dài 10 m. Tính chiều dài và chiều rộng của mảnh đất hình chữ nhật đó.

Hướng dẫn giải:

Nửa chu vi của mảnh đất là: 28 : 2 = 14 (m).

Gọi chiều dài của mảnh đất là x (m).

Chiều rộng của mảnh đất là 14 – x (m).

Độ dài đường chéo của mảnh đất là 10 m nên ta có phương trình:

x² + (14 – x)² = 10²

x² + 196 – 28x + x² = 100

2x² – 28x + 96 = 0

Ta có: ∆ = 28² – 4 . 2 . 96 = 16 > 0 nên phương trình có hai nghiệm phân biệt.

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-\left(-28\right)+\sqrt{16}}{2.2}=8;$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-\left(-28\right)-\sqrt{16}}{2.2}=6.$

• Nếu chiều dài là 8 m thì chiều rộng là 14 – 8 = 6 (m)

• Nếu chiều dài là 6 m thì chiều rộng là 14 – 6 = 8 (m) (loại).

Vậy chiều dài và chiều rộng mảnh đất lần lượt là 8 m và 6 m.

Bài 13. Tìm hai số biết tổng của chúng bằng 25 và tích của chúng bằng 60.

Hướng dẫn giải

Hai số cần tìm là nghiệm của phương trình x² – 25x + 60 = 0.

Ta có: ∆ = 25² – 4 . 1 . 60 = 385 > 0 nên phương trình có 2 nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-\left(-25\right)+\sqrt{385}}{2.1}=\frac{25+\sqrt{385}}{2};$

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-\left(-25\right)-\sqrt{385}}{2.1}=\frac{25-\sqrt{385}}{2}.$

Vậy hai số cần tìm là $\frac{25+\sqrt{385}}{2}$ và $\frac{25-\sqrt{385}}{2}$.

Bài 14. Cho phương trình –3x² – 5x – 2 = 0. Với x₁, x₂ là nghiệm của phương trình, không giải phương trình hãy tính giá trị của các biểu thức $M=x_1+\frac{1}{x_1}+\frac{1}{x_2}+x_2$.

Hướng dẫn giải

Áp dụng hệ thức Viète, ta có:

$S=x_1+x_2=-\frac{b}{a}=-\frac{-5}{-3}=-\frac{5}{3};$

$P=x_1.x_2=\frac{c}{a}=\frac{-2}{-3}=\frac{2}{3}$.

Ta có: $M=x_1+\frac{1}{x_1}+\frac{1}{x_2}+x_2$ $=x_1+x_2+\frac{1}{x_1}+\frac{1}{x_2}$

             $=\left(x_1+x_2\right)+\frac{x_1+x_2}{x_1.x_2}$ $=-\frac{5}{3}+\frac{-\frac{5}{3}}{\frac{2}{3}}$

Bài 15. Cho phương trình x² + 5 mx − 4 = 0. Tìm m để x₁, x₂  là nghiệm của phương trình và thỏa mãn: x₁² + x₂² + 6x₁x₂ = 9.

Hướng dẫn giải

Xét phương trình x² + 5mx − 4 = 0  (*) 

Để phương trình (*) có nghiệm khi và chỉ khi: 

Δ = (5m)² − 4.1. (− 4) = 25m² + 16 > 0.

Mà  m² ≥ 0 với mọi m nên Δ = 25m² + 16 > 0 với mọi m. 

Do đó, phương trình (*) có nghiệm với mọi m.

Gọi hai nghiệm của phương trình là x₁, x₂.

Áp dụng hệ thức Viète, ta có:

$S=x_1+x_2=-\frac{5m}{1}=-5m$;

$P=x_1.x_2=\frac{c}{a}=\frac{-4}{1}=-4.$

Mặt khác, ta có: x₁² + x₂² + 6x₁x₂ = 9   

x₁² + 2x₁x₂ + x₂² + 4x₁x₂ = 9 

(x₁ + x₂)² + 4x₁x₂ = 9 

(−5m)² + 4. (−4) = 9 

25m² − 16 = 9 

25m² = 25 

m² = 1 

m = ± 1.

Vậy m = 1 hoặc m = –1 thì phương trình có hai nghiệm x₁, x₂ thỏa mãn thỏa mãn yêu cầu bài toán.

Học tốt Toán 9 Chương 6

Các bài học để học tốt Bài tập cuối chương 6 Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài tập cuối chương 6