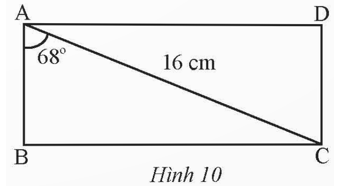
Tính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và góc BAC = 68 độ (Hình 10).
Câu hỏi:
Tính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và (Hình 10).
Trả lời:
Xét tam giác ABC vuông tại B có , ta có:
•
•
Vì ABCD là hình chữ nhật nên ta có AB = CD = 6 cm và BC = AD = 14,8 cm.
Vậy độ dài các cạnh của hình chữ nhật ABCD là AB = 6 cm và BC = 14,8 cm, CD = 6 cm, AD = 14,8 cm.