Giải Toán 9 trang 12 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 9 trang 12 Tập 1 trong Bài 2: Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 12.

Giải Toán 9 trang 12 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 12 Toán 9 Tập 1: Xác định các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn sau:

a) x + 5y = –4;

b) $\sqrt{3}x+y=0$;

c) $0x-\frac{3}{2}y=6$;

d) 2x + 0y = –1,5.

Lời giải:

a) x + 5y = –4 là phương trình bậc nhất hai ẩn với a = 1, b = 5, c = –4.

b) $\sqrt{3}x+y=0$ là phương trình bậc nhất hai ẩn với $a=\sqrt{3},b=\mathrm{1,}c=0$.

c) $0x-\frac{3}{2}y=6$ là phương trình bậc nhất hai ẩn với $a=\mathrm{0,}b=-\frac{3}{2},c=6$.

d) 2x + 0y = –1,5 là phương trình bậc nhất hai ẩn với a = 2, b = 0, c = –1,5.

Thực hành 2 trang 12 Toán 9 Tập 1: Cho phương trình 3x + 2y = 4. (1)

a) Trong hai cặp số (1; 2) và (2; –1), cặp số nào là nghiệm của phương trình (1)?

b) Tìm y₀ để cặp số (4; y₀) là nghiệm của phương trình (1).

c) Tìm thêm hai nghiệm của phương trình (1).

d) Hãy biểu diễn tất cả các nghiệm của phương trình (1) trên mặt phẳng tọa độ Oxy.

Lời giải:

a) Cặp số (1; 2) không phải là nghiệm của phương trình (1) vì 3 . 1 + 2 . 2 = 3 + 4 = 7 ≠ 4.

Cặp số (–2; 5) là nghiệm của phương trình (1) vì 3 . (–2) + 2 . 5 = –6 + 10 = 4.

Vậy trong hai cặp số đã cho, cặp số (–2; 5) là nghiệm của phương trình (1).

b) Để cặp số (4; y₀) là nghiệm của phương trình (1) thì

3 . 4 + 2y₀ = 4 hay 12 + 2y₀ = 4 suy ra y₀ = –4.

c) Tìm thêm hai nghiệm của phương trình (1).

• Thay x = 0 vào phương trình (1), ta có:

3 . 0 + 2y = 4 hay 2y = 4 suy ra y = 2.

• Thay x = 2 vào phương trình (1), ta có:

3 . 2 + 2y = 4 hay 6 + 2y = 4 suy ra y = –1.

Vậy hai nghiệm của phương trình (1) khác với các nghiệm trên là (0; 2) và (2; –1).

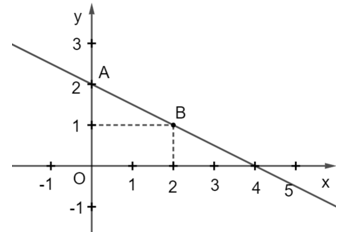
d) Phương trình (1) có nghiệm là (0; 2) và (2; –1) nên đường thẳng 3x + 2y = 4 đi qua hai điểm A(0; 2) và B(2; –1).

Vậy ta có biểu diễn tất cả các nghiệm của phương trình (1) trên mặt phẳng tọa độ Oxy như sau:

Khám phá 2 trang 12 Toán 9 Tập 1: Một ô tô từ A đến B, cùng lúc đó một xe máy đi từ B về A. Gọi x (km/h) là tốc độ của ô tô, y (km/h) là tốc độ của xe máy (x > 0, y > 0). Biết rằng:

(1) Tốc độ của ô tô hơn tốc độ xe máy 15 km/h;

(2) Quãng đường AB dài 210 km và hai xe gặp nhau sau 2 giờ.

a) Từ dữ kiện (1), hãy lập một phương trình hai ẩn x, y?

b) Từ dữ kiện (2), hãy lập thêm một phương trình hai ẩn x, y?

c) Bạn An khẳng định rằng tốc độ của ô tô và xe máy lần lượt là 60 km/h và 45 km/h. Có thể dùng hai phương trình lập được để kiểm tra khẳng định của bạn An là đúng hay sai không?

Lời giải:

a) Từ dữ kiện (1), ta lập được phương trình là: x – y = 15.          (3)

b) Quãng đường đi được của ô tô sau 2 giờ là: 2x (km)

Quãng đường đi được của xe máy sau 2 giờ là: 2y (km)

Một ô tô từ A đến B, cùng lúc đó một xe máy đi từ B về A nghĩa là ô tô và xe máy chuyển động ngược chiều nên 2x + 2y = 210 (km).

Vậy từ dữ kiện (2), ta lập được phương trình là: 2x + 2y = 210 hay x + y = 105.      (4)

c) Khi tốc độ của ô tô và xe máy lần lượt là 60 km/h và 45 km/h thì x = 60 km/h và y = 45 km/h.

• Thay x = 60, y = 45 vào phương trình (3), ta có:

x – y = 60 – 45 = 15.

• Thay x = 60, y = 45 vào phương trình (4), ta có:

x + y = 60 + 45 = 105.

Vậy ta có thể dùng hai phương trình lập được để kiểm tra khẳng định của bạn An và ta thấy khẳng định của bạn An là đúng.

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 Bài 2: Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn hay khác:

• Giải Toán 9 trang 10
• Giải Toán 9 trang 14