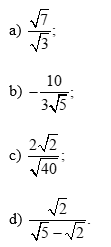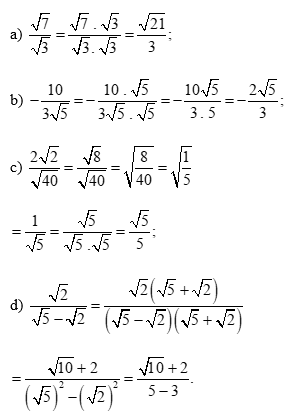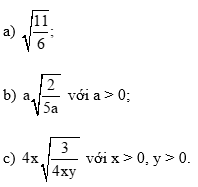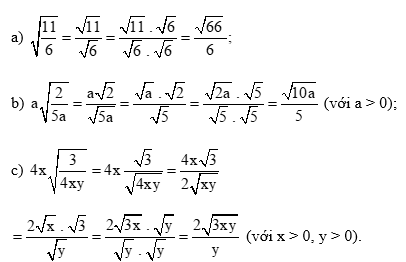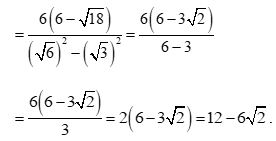Giải Toán 9 trang 54 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 9 trang 54 Tập 1 trong Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai Toán 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 54.

Giải Toán 9 trang 54 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 54 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:

Lời giải:

Thực hành 2 trang 54 Toán 9 Tập 1: Khử mẫu của biểu thức lấy căn:

Lời giải:

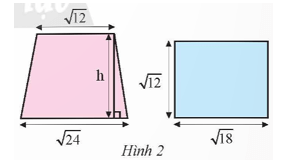
Vận dụng 1 trang 54 Toán 9 Tập 1: Biết rằng hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau. Tính chiều cao h của hình thang.

Lời giải:

Diện tích hình chữ nhật là:

$\sqrt{18}.\sqrt{12}=\sqrt{18.12}=\sqrt{18.2.6}=\sqrt{36.6}=6\sqrt{6}$(đvdt).

Vì hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau nên diện tích hình thang bằng $6\sqrt{6}$(đvdt).

Khi đó, diện tích hình thang là: $\frac{\sqrt{24}+ \sqrt{12}}{2}.h= 6\sqrt{6}$.

Ta có $\frac{\sqrt{24}+ \sqrt{12}}{2}=\frac{\sqrt{4.6}+\sqrt{4.3}}{2}$

$=\frac{2\sqrt{6}+2\sqrt{3}}{2}=\frac{2\left(\sqrt{6}+\sqrt{3}\right)}{2}=\sqrt{6}+\sqrt{3}$.

Do đó,$\left(\sqrt{6}+\sqrt{3}\right).h=6\sqrt{6}$

Suy ra  h = $\frac{6\sqrt{6}}{\sqrt{6}+\sqrt{3}}=\frac{6\sqrt{6}\left(\sqrt{6}-\sqrt{3}\right)}{\left(\sqrt{6}+\sqrt{3}\right)\left(\sqrt{6}-\sqrt{3}\right)}$

Vậy chiều cao h của hình thang $h = 12 - 6\sqrt{2}$.

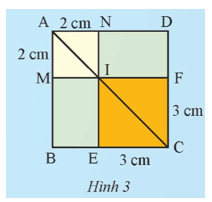
Khám phá 2 trang 54 Toán 9 Tập 1: Hình vuông ABCD được chia thành hai hình vuông và hai hình chữ nhật như Hình 3.

a) Tính độ dài đường chéo của hai hình vuông AMIN và CEIF.

b) Tính độ dài đường chéo của hình vuông ABCD theo hai cách khác nhau.

Lời giải:

a) Vì AMIN là hình vuông nên AM = IN = 2 cm, $\widehat{ANI}= {90}^o$.

Xét tam giác ANI vuông tại N, áp dụng định lí Pythagore, ta có

AI² = AN² + IN² = 2² + 2² = 8.

Suy ra $AI = \sqrt{8} = 2\sqrt{2}\left(cm\right)$.

Vì CEIF là hình vuông nên IE = CF = 3 cm, $\widehat{IEC}= {90}^o$.

Xét tam giác IEC vuông tại E, áp dụng định lí Pythagore, ta có

IC² = IE² + EC² = 3² + 3² = 18.

Suy ra $IC = \sqrt{18} = 3\sqrt{2} \left(cm\right)$

Vậy độ dài đường chéo của hai hình vuông AMIN và CEIF  lần lượt là $2\sqrt{2} cm$ và $3\sqrt{2} cm$

b)

Cách 1: Độ dài đường chéo hình vuông là:

AC = AI + IC = $2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2}$

Cách 2:

• Vì BMIE là hình chữ nhật nên BM = IE = 3 cm.

• Vì DNIF là hình chữ nhật nên IN = DF = 2 cm.

Độ dài cạnh AB là: AB = AM + BM = 2 + 3 = 5 (cm).

Độ dài cạnh BC là: BC = BE + EC = 2 + 3 = 5 (cm).

Vì ABCD là hình vuông nên $\widehat{BAC}= {90}^o$ , suy ra tam giác ABC vuông tại B.

Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore, ta có

AC² = AB² + BC² = 5² + 5² = 50.

Suy ra $AC = \sqrt{50} = 5\sqrt{2}$ (cm).

Vậy độ dài đường chéo của hình vuông ABCD là $5\sqrt{2} cm$.

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay khác:

• Giải Toán 9 trang 52
• Giải Toán 9 trang 56