Bài 4.19 trang 80 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

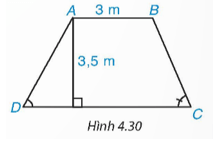
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là tanD = 1,25. Độ dốc của sườn BC, tức là tanC = 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).

Giải Toán 9 Luyện tập chung - Kết nối tri thức

Bài 4.19 trang 80 Toán 9 Tập 1: Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là tanD = 1,25. Độ dốc của sườn BC, tức là tanC = 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).

Lời giải:

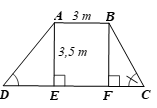
Kẻ AE ⊥ CD, BF ⊥ CD. Khi đó AE // BF.

Vì ABCD là hình thang nên AB // CD, do đó suy ra AB // EF.

Xét tứ giác ABFE có: AE // BF và AB // EF nên là hình bình hành.

Lại có $\widehat{E}=90°,$ nên hình bình hành ABFE là hình chữ nhật.

Suy ra EF = AB = 3 m.

Xét ∆ADE vuông tại E, ta có:

$\tan D=\frac{AE}{DE},$ suy ra $DE=\frac{AE}{\tan D}=\frac{\mathrm{3,5}}{\mathrm{1,25}}=\mathrm{2,8}\text{ (m).}$

Vì ABFE là hình chữ nhật nên BF = AE = 3,5 m.

Xét ∆BCF vuông tại F, ta có:

$\tan C=\frac{BF}{FC},$ suy ra $FC=\frac{BF}{\tan C}=\frac{\mathrm{3,5}}{\mathrm{1,5}}=\frac{7}{3}\text{ (m).}$

Ta có: $DC=DE+EF+FC=\mathrm{2,8}+3+\frac{7}{3}=\frac{122}{15}=\text{8,1}\left(3\right)\text{ (m)}\approx 81\text{ (dm).}$

Xét ∆ADE vuông tại E, theo định lí Pythagore, ta có:

AD² = AE² + DE² = 3,5² + 2,8² = 20,09.

Suy ra $AD=\sqrt{\mathrm{20,09}}\approx \mathrm{4,482186966...}\text{ (m)}\approx \text{45 (dm).}$

Xét ∆BCF vuông tại F, theo định lí Pythagore, ta có:

$B{C}^2=B{F}^2+C{F}^2={\mathrm{3,5}}^2+{\left(\frac{7}{3}\right)}^2=\frac{637}{36}.$

Suy ra $BC=\sqrt{\frac{637}{36}}=\mathrm{4,206476388...}\text{ (m)}\approx 42\text{ (dm).}$

Lời giải bài tập Toán 9 Luyện tập chung hay, chi tiết khác:

• Bài 4.14 trang 80 Toán 9 Tập 1: Một cuốn sách khổ 17 × 24 cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi α là góc ....

• Bài 4.15 trang 80 Toán 9 Tập 1: Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết HB = 3 cm, HC = 6 cm ....

• Bài 4.16 trang 80 Toán 9 Tập 1: Tìm chiều rộng d của dòng sông trong Hình 4.27 (làm tròn đến m) ....

• Bài 4.17 trang 80 Toán 9 Tập 1: Tính các số liệu còn thiếu (dấu "?") ở Hình 4.28 với góc làm tròn đến độ ....

• Bài 4.18 trang 80 Toán 9 Tập 1: Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước ....

• Bài 4.20 trang 80 Toán 9 Tập 1: Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển ....