Bài 5.21 trang 103 Toán 9 Kết nối tri thức Tập 1
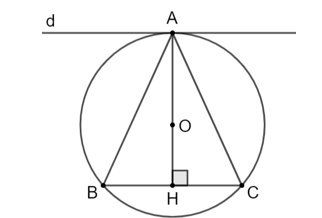
Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).
Giải Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn - Kết nối tri thức
Bài 5.21 trang 103 Toán 9 Tập 1: Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).
Lời giải:
Ta có đường thẳng AO là trục đối xứng của đường tròn.
Nên B là điểm đối xứng của C qua AO.
Gọi H là giao điểm của AO và BC.
Khi đó ta có: AH ⊥ BC mà d // BC nên AH ⊥ d.
Vậy d là một tiếp tuyến của đường tròn.
Lời giải bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn hay, chi tiết khác: