HĐ4 trang 102 Toán 9 Kết nối tri thức Tập 1

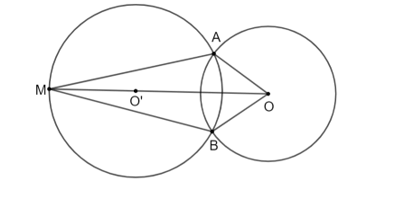
(Dựa vào hình vẽ có được sau HĐ3). Bằng cách xét hai tam giác OMA và OMB, chứng minh rằng:

Giải Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn - Kết nối tri thức

HĐ4 trang 102 Toán 9 Tập 1: (Dựa vào hình vẽ có được sau HĐ3). Bằng cách xét hai tam giác OMA và OMB, chứng minh rằng:

a) MA = MB;

b) MO là tia phân giác của góc AMB;

c) OM là tia phân giác của góc AOB.

Lời giải:

HĐ4 trang 102 Toán 9 Kết nối tri thức Tập 1

a) Xét hai tam giác vuông OAM và OBM có:

OA = OB; OM chung

Do đó ΔOAM = ΔOBM (cạnh huyền – cạnh góc vuông).

Suy ra AM = BM (hai cạnh tương ứng).

b) Vì ΔOAM = ΔOBM (câu a) nên $\hat{O A M} = \hat{O B M}$ (hai góc tương ứng).

Suy ra OM là tia phân giác của góc AMB.

c) Vì ΔOAM = ΔOBM (câu a) nên $\hat{A O M} = \hat{B O M}$ (hai góc tương ứng).

Suy ra Om là tia phân giác của góc AOB.

Lời giải bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn hay, chi tiết khác: