Bài 5.22 trang 103 Toán 9 Kết nối tri thức Tập 1
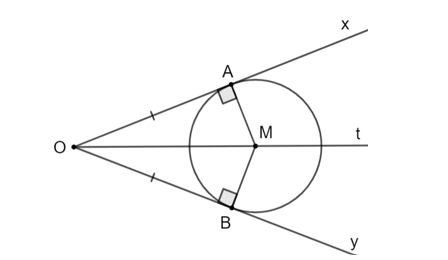
Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).
Giải Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn - Kết nối tri thức
Bài 5.22 trang 103 Toán 9 Tập 1: Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).
Lời giải:
Xét ΔOAM và ΔOBM có:
OM chung
(do OM là tia phân giác của góc )
OA = OB
Do đó ΔOAM = ΔOBM (c.g.c).
Suy ra AM = BM (hai cạnh tương ứng).
Và (hai góc tương ứng) hay OB ⊥ MB.
Do đó OA là tiếp tuyến của đường tròn (M; MA).
Vậy OA và OB là hai tiếp tuyến cắt nhau của (O).
Lời giải bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn hay, chi tiết khác: