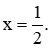Giải phương trình 1/ x-1 - 4x/ x^3 -1= x / x^2 + x+1
Câu hỏi:
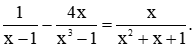
Trả lời:
Ta có:
⦁ x – 1 ≠ 0 khi x ≠ 1.
⦁ 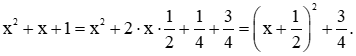
Với mọi x ta luôn có 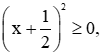 nên
nên 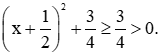
⦁ x3 – 1 = (x – 1)(x2 + x + 1).
Khi đó x3 – 1 ≠ 0 khi (x – 1)(x2 + x + 1) ≠ 0, hay x – 1 ≠ 0, tức là x ≠ 1.
Vì vậy, điều kiện xác định của phương trình đã cho là x ≠ 1.
Quy đồng mẫu của phương trình, ta được:
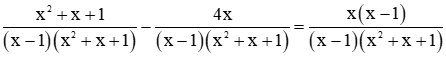
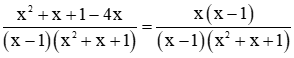
Khử mẫu của phương trình, ta được: x2 + x + 1 – 4x = x(x – 1). (*)
Giải phương trình (*):
x2 + x + 1 – 4x = x(x – 1)
x2 – 3x + 1 = x2 – x
x2 – 3x + 1 – x2 + x = 0
–2x = –1
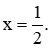
Giá trị 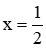 thỏa mãn điều kiện xác định của phương trình.
thỏa mãn điều kiện xác định của phương trình.
Vậy phương trình đã cho có nghiệm là