Lý thuyết Toán lớp 9 Tứ giác nội tiếp - Kết nối tri thức
Haylamdo biên soạn tóm tắt lý thuyết Toán 9 Bài 29: Tứ giác nội tiếp sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.
Lý thuyết Toán lớp 9 Tứ giác nội tiếp - Kết nối tri thức
Lý thuyết Tứ giác nội tiếp
1. Đường tròn ngoại tiếp một tứ giác
1.1. Đường tròn đi qua bốn đỉnh của một tứ giác
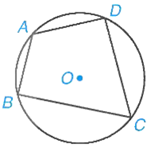
Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (hoặc đơn giản là tứ giác nội tiếp) và đường tròn được gọi là đường tròn ngoại tiếp tứ giác.
Cụ thể, ở hình vẽ trên, tứ giác ABCD được gọi là nội tiếp đường tròn (O) và ta cũng nói đường tròn (O) ngoại tiếp tứ giác ABCD.
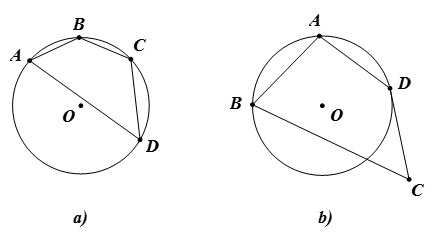
Ví dụ 1. Trong các hình sau, hình nào biểu diễn tứ giác ABCD nội tiếp đường tròn (O)?
Hướng dẫn giải
– Ở Hình a), ta có tứ giác ABCD nội tiếp đường tròn (O) vì cả bốn đỉnh A, B, C, D đều nằm trên đường tròn (O).
– Ở Hình b), ta có tứ giác ABCD không nội tiếp đường tròn (O) vì đỉnh C không nằm trên đường tròn (O).
1.2. Định lí về tổng số đo các góc đối nhau của một tứ giác nội tiếp
Định lí: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180°.
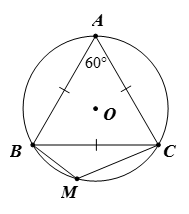
Ví dụ 2. Cho đường tròn (O) ngoại tiếp tam giác đều ABC. Lấy điểm M thuộc cung nhỏ BC (M ≠ B, C). Tính số đo
Hướng dẫn giải
Vì tam giác ABC đều nên
Ta có tứ giác ABMC nội tiếp đường tròn (O) nên
Do đó
Vậy
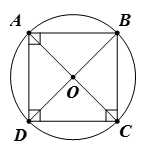
2. Đường tròn ngoại tiếp hình chữ nhật và hình vuông
Hình chữ nhật và hình vuông là các tứ giác nội tiếp. Đường tròn ngoại tiếp của chúng có tâm là giao điểm của hai đường chéo và bán kính bằng một nửa độ dài đường chéo.
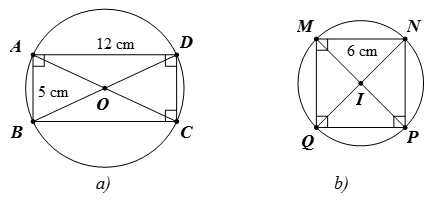
Ví dụ 3. Xác định tâm và tính bán kính:
a) Hình chữ nhật ABCD có AB = 5 cm và AD = 12 cm.
b) Hình vuông MNPQ có MN = 6 cm.
Hướng dẫn giải
a) Gọi O là giao điểm của hai đường chéo AC và BD.
Suy ra O là tâm đường tròn ngoại tiếp của hình chữ nhật ABCD.
Áp dụng định lí Pythagore cho tam giác ABD vuông tại A, ta được:
BD2 = AB2 + AD2 = 52 + 122 = 169.
Suy ra BD = 13 (cm).
Do đó, bán kính đường tròn ngoại tiếp hình chữ nhật ABCD là:
(cm).
Vậy đường tròn ngoại tiếp hình chữ nhật ABCD có tâm O là giao điểm của AC, BD và bán kính R = 6,5 cm.
b) Gọi I là giao điểm của hai đường chéo MP và NQ.
Suy ra I là tâm đường tròn ngoại tiếp hình vuông MNPQ.
Vì MNPQ là hình vuông nên MQ = MN = 6 cm.
Áp dụng định lí Pythagore cho tam giác MNQ vuông tại M, ta được:
NQ2 = MN2 + MQ2 = 62 + 62 = 72.
Suy ra (cm).
Do đó, bán kính đường tròn ngoại tiếp hình vuông MNPQ là:
(cm).
Vậy đường tròn ngoại tiếp hình vuông MNPQ có tâm I là giao điểm của MP, NQ và bán kính cm.
Bài tập Tứ giác nội tiếp
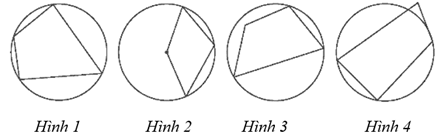
Bài 1. Trong các hình sau, hình nào biểu diễn tứ giác nội tiếp đường tròn?
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Hướng dẫn giải
Đáp án đúng là: A
Hình 1 biểu diễn tứ giác nội tiếp đường tròn vì tứ giác có bốn đỉnh nằm trên đường tròn.
Hình 2, 3, 4 không biểu diễn tứ giác nội tiếp đường tròn vì mỗi tứ giác đều có một đỉnh không nằm trên đường tròn.
Vậy ta chọn phương án A.
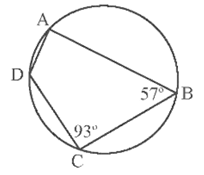
Bài 2. Cho hình vẽ dưới đây.
Khi đó số đo các góc lần lượt bằng
A. 60° và 115°;
B. 90° và 120°;
C. 87° và 123°;
D. 123° và 87°.
Hướng dẫn giải
Đáp án đúng là: C
Ta có tứ giác ABCD nội tiếp đường tròn nên:
⦁
Do đó
⦁
Do đó
Vậy
Do đó ta chọn phương án C.
Bài 3. Độ dài cạnh của hình vuông ABCD nội tiếp đường tròn là
A. dm;
B. dm;
C. 10 dm;
D. 20 dm.
Hướng dẫn giải
Đáp án đúng là: D
Vì hình vuông ABCD nội tiếp đường tròn nên (dm).
Suy ra (dm).
Vì ABCD là hình vuông nên AB = AD.
Áp dụng định lí Pythagore cho tam giác ABD vuông tại A, ta được:
AB2 + AD2 = BD2.
Suy ra hay 2AB2 = 800, nên AB2 = 400
Do đó AB = 20 (dm) (do AB > 0).
Vậy ta chọn phương án D.
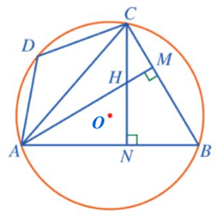
Bài 4. Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho tam giác ABC nhọn. Hai đường cao AM, CN của tam giác ABC cắt nhau tại H. Chứng minh:
a)
b)
c)
Hướng dẫn giải
a) Ta có (do AM, CN là hai đường cao cắt nhau tại H của tam giác ABC).
Do đó hai điểm M, N cùng nằm trên đường tròn đường kính HB.
Khi đó tứ giác HMBN nội tiếp đường tròn đường kính HB.
Vậy hay
b) Ta có tứ giác ABCD nội tiếp đường tròn (O) nên
Mà (câu a) nên
Lại có (cặp góc đối đỉnh) nên
c) Tam giác ABM, có: (tổng ba góc của một tam giác)
Mà (chứng minh trên)
Suy ra <![endif]>
Vậy
Bài 5. Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên đoạn AC, đường tròn đường kính CM cắt hai đường thẳng BM và BC lần lượt tại D và N. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp.
b) Các đường thẳng AB, MN, CD cùng đi qua một điểm.
Hướng dẫn giải
a) Gọi I là trung điểm BC. Khi đó,
Ta có (góc nội tiếp chắn nửa đường tròn đường kính CM).
Suy ra tam giác BCD vuông tại D.
Do đó (tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông). Suy ra IB = IC = ID.
Tương tự đối với ∆ABC vuông tại A, ta cũng có IA = IB = IC.
Do đó, IA = IB = IC = ID.
Vậy tứ giác ABCD nội tiếp đường tròn tâm I, đường kính BC.
b) Ta có (góc nội tiếp chắn nửa đường tròn đường kính CM).
Suy ra MN ⊥ BC.
Xét ∆BMC có: MN ⊥ BC, CD ⊥ BM và AB ⊥ MC nên AB, MN, CD là ba đường cao của tam giác, do đó ba đường cao AB, MN, CD cắt nhau tại trực tâm K của tam giác BMC.
Vậy các đường thẳng AB, MN, CD cùng đi qua một điểm.
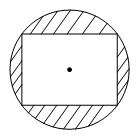
Bài 6. Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 6 cm và 4 cm (như hình vẽ).
Tính diện tích phần bị gạch chéo (làm tròn kết quả đến hàng phần trăm).
Hướng dẫn giải
Áp dụng định lí Pythagore, ta có độ dài đường chéo của hình chữ nhật là:
(cm).
Hình chữ nhật nội tiếp đường tròn nên đường kính của đường tròn chính là độ dài của đường chéo hình chữ nhật.
Bán kính đường tròn là: (cm).
Diện tích hình chữ nhật là: Shcn = 6.4 = 24 (cm2).
Diện tích hình tròn là: Shình tròn = πR2 = 13π (cm2).
Diện tích phần bị gạch chéo là: S = Stròn – Shcn = 13π – 24 ≈ 16,84 (cm2).
Vậy diện tích phần bị gạch chéo bằng khoảng 16,84 cm2.
Học tốt Tứ giác nội tiếp
Các bài học để học tốt Tứ giác nội tiếp Toán lớp 9 hay khác: