Lý thuyết Toán lớp 9 Hình trụ và hình nón - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 9 Bài 31: Hình trụ và hình nón sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán lớp 9 Hình trụ và hình nón - Kết nối tri thức

Lý thuyết Hình trụ và hình nón

1. Hình trụ

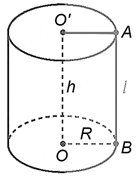
− Một số yếu tố của hình trụ:

Chiều cao: h = O'O.

Bán kính đáy: R = OB.

Đường sinh: l = AB.

− Diện tích xung quanh của hình trụ: $S_{xq}=2\pi Rh$.

Trong đó: R là bán kính đáy;

  h là chiều cao.

− Thể tích hình trụ: V = S_đáy . h = πR²h.

Trong đó: S_đáy là diện tích đáy;

  R là bán kính đáy;

  h là chiều cao.

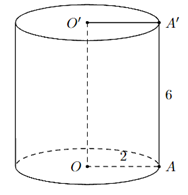
Ví dụ: Xét hình trụ dưới đây với bán kính đáy là 2 cm, chiều cao 6 cm (như hình vẽ).

Tính diện tích xung quanh và thể tích của hình trụ.

Hướng dẫn giải

Diện tích xung quanh của hình trụ là:

S_xq = 2πRh = 2π . 2 . 6 = 24π (cm²)

Thể tích hình trụ là:

V = πR²h = π. 2² . 6 = 24π (cm³)

2. Hình nón

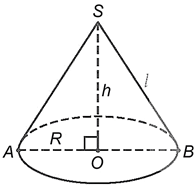
− Một số yếu tố của hình nón:

Đỉnh: S.

Chiều cao: h = SO.

Đường sinh: l = SA = SB.

Bán kính đáy: R = OA.

− Diện tích xung quanh của hình nón: S_xq = πrl.

Trong đó: r là bán kính đáy;

  l là độ dài đường sinh.

− Thể tích hình nón: $V=\frac{1}{3}.S_{dáy}.h=\frac{1}{3}\pi r^{2}h.$

Trong đó: S_đáy là diện tích đáy;

  r là bán kính đáy;

  h là chiều cao.

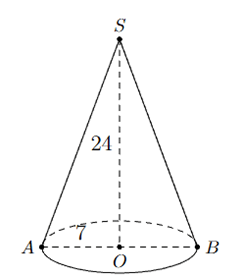
Ví dụ: Xét một hình nón có bán kính đáy bằng 7 cm, chiều cao bằng 24 cm như sau:

Tính diện tích xung quanh và thể tích của hình nón.

Hướng dẫn giải

Áp dụng định lý Pythagore, ta tính được độ dài đường sinh hình nón:

$l=\sqrt{{\text{R}}^2+{\text{h}}^{\text{2}}}=\sqrt{7^2+{24}^2}=25$ (cm).

Diện tích xung quanh của hình nón là:

S_xq = πrl = π . 7 . 25 = 175π (cm²).

Thể tích hình nón là:

$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi {.7}^2.27=392\pi$(cm³).

Bài tập Hình trụ và hình nón

Bài 1. Một hình trụ có diện tích xung quanh là 20π cm² và diện tích toàn phần là 28π cm² . Tính thể tích của hình trụ đó.

A. 20π cm³.

B. 22π cm³.

C. 24π cm³.

D. 25π cm³.

Hướng dẫn giải

Đáp án đúng là: A

Ta có S_đáy = $\frac{S_{tp}-S_{xq}}{2}=\frac{28\pi -20\pi }{2}=4\pi$(cm²)

Mà S_đáy = πR² nên 4π = πR² hay R = 2 (cm).

Lại có S_xq = 2πRh hay $h=\frac{20\pi }{2\pi R}=\frac{10}{2}=5$ (cm)

Thể tích của hình trụ đó là:

V = πR²h = π. 2² . 5 = 20π (cm³).

Bài 2. Một hình nón có bán kính đáy bằng r, diện tích xung quanh gấp đôi diện tích đáy. Diện tích xung quanh của hình nón tính theo r là

A. πrl.

B. 2πr².

C. 2πr.

D. πr²l.

Hướng dẫn giải

Đáp án đúng là: B

Diện tích xung quanh gấp đôi diện tích đáy nên πrl = 2πr².

Suy ra l = 2r.

Do đó πrl = πr · 2r = 2πr².

Vậy diện tích xung quanh bằng 2πr².

Bài 3. Một hình trụ có chiều cao bằng 5 cm. Biết diện tích toàn phần gấp đôi diện tích xung quanh. Tính thể tích hình trụ.

Hướng dẫn giải

Vì diện tích toàn phần bằng hai lần diện tích xung quanh nên

2πRh + 2πR² = 4πRh nên 2πR² = 2πRh hay R = h.

Do đó, bán kính đáy là 5 cm.

Thể tích của hình trụ là:

V = πR²h = π · 5² · 5 = 125π (cm³).

Vậy thể tích hình trụ là 125π cm³.

Bài 4. Một hình nón có bán kính đáy bằng 20 cm, số đo thể tích (tính bằng cm²) bằng bốn lần số đo diện tích xung quanh (tính bằng cm²). Tính chiều cao của hình nón.

Hướng dẫn giải

Gọi h là chiều cao của hình nón.

Thể tích của hình nón bằng:

$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi .{20}^2.h=\frac{400}{3}\pi h$.

Đường sinh SA bằng $\sqrt{h^2+{20}^2}=\sqrt{h^2+400}$ .

Diện tích xung quanh của hình nón bằng:

$S_{xq}=\pi .20.\sqrt{h^2+400}$.

Do V = 4S_xq nên $\frac{400}{3}\pi h=4\pi .20.\sqrt{h^2+400}$

  $5h=3\sqrt{h^2+400}$

  $5h^2=9\left(h^2+400\right)$

  h = 15 (cm)

Vậy chiều cao của hình nón bằng 15 cm.

Bài 5. Một thùng phuy hình trụ có số đo diện tích xung quanh (tính bằng mét vuông) đúng bằng số đo thể tích (tính bằng mét khối). Tính bán kính đáy của thùng phuy.

Hướng dẫn giải

Gọi bán kính đáy và chiều cao thùng phuy lần lượt là R và h.

Ta có S_xq = 2πRh (m²);

  V = πR²h (m³).

Theo đề bài hai số đo trên bằng nhau nên ta có 2πRh = πR²h.

Suy ra R = 2 (m).

Vậy bán kính đáy của thùng phuy là 2 m.

Học tốt Hình trụ và hình nón

Các bài học để học tốt Hình trụ và hình nón Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài 31: Hình trụ và hình nón