Lý thuyết Toán lớp 9 Bài tập cuối chương 9 - Kết nối tri thức

---

Haylamdo tổng hợp lý thuyết Toán 9 Chương 9: Đường tròn ngoại tiếp và đường tròn nội tiếp sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm Toán 9 Chương 9.

Lý thuyết Toán lớp 9 Bài tập cuối chương 9 - Kết nối tri thức

Tổng hợp lý thuyết Toán 9 Chương 9

1. Định nghĩa góc nội tiếp và cung bị chắn

Định nghĩa góc nội tiếp: Góc nội tiếp của đường tròn là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Định nghĩa cung bị chắn: Cung nằm bên trong góc được gọi là cung bị chắn.

2. Định lí liên hệ giữa góc nội tiếp với cung bị chắn

Định lí: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

Nhận xét: Từ định lí trên ta có các khẳng định sau đối với các góc nội tiếp của một đường tròn hoặc của hai đường tròn bằng nhau:

⦁ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

⦁ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

⦁ Các góc nội tiếp chắn cung nhỏ thì có số đo bằng nửa số đo của góc ở tâm chắn cùng một cung.

⦁ Góc nội tiếp chắn nửa đường tròn là góc vuông.

3. Đường tròn ngoại tiếp một tam giác

3.1. Khái niệm đường tròn ngoại tiếp tam giác

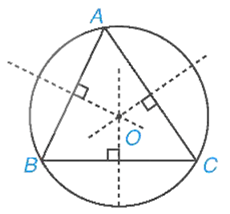
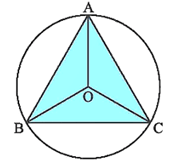
Định nghĩa: Đường tròn ngoại tiếp một tam giác là đường tròn đi qua ba đỉnh của tam giác đó.

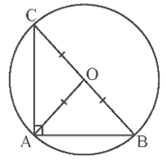
Trong hình vẽ trên, đường tròn (O; OA) ngoại tiếp tam giác ABC. Ta cũng nói tam giác ABC nội tiếp đường tròn (O), hay (O) là đường tròn ngoại tiếp tam giác ABC. Tâm O là giao điểm của ba đường trung trực của tam giác ABC.

3.2. Đường tròn ngoại tiếp tam giác vuông

Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng một nửa cạnh huyền.

3.3. Đường tròn ngoại tiếp tam giác đều

Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng $\frac{\sqrt{3}}{3}a.$

4. Đường tròn nội tiếp một tam giác

4.1. Đường tròn nội tiếp tam giác

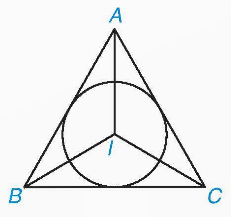
Định nghĩa: Đường tròn tiếp xúc với ba cạnh của tam giác được gọi là đường tròn nội tiếp tam giác. Tam giác đó được gọi là ngoại tiếp đường tròn. Tâm đường tròn nội tiếp tam giác là giao điểm ba đường phân giác của tam giác.

Chú ý: Đường tròn tiếp xúc với một cạnh của tam giác nghĩa là tiếp xúc với đường thẳng chứa cạnh đó và có tiếp điểm nằm trên cạnh đó.

4.2. Đường tròn nội tiếp tam giác đều

Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng $\frac{\sqrt{3}}{6}a.$

5. Đường tròn ngoại tiếp một tứ giác

5.1. Đường tròn đi qua bốn đỉnh của một tứ giác

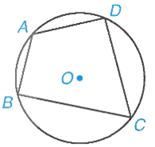
Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (hoặc đơn giản là tứ giác nội tiếp) và đường tròn được gọi là đường tròn ngoại tiếp tứ giác.

Cụ thể, ở hình vẽ trên, tứ giác ABCD được gọi là nội tiếp đường tròn (O) và ta cũng nói đường tròn (O) ngoại tiếp tứ giác ABCD.

5.2. Định lí về tổng số đo các góc đối nhau của một tứ giác nội tiếp

Định lí: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180°.

6. Đường tròn ngoại tiếp hình chữ nhật và hình vuông

Hình chữ nhật và hình vuông là các tứ giác nội tiếp. Đường tròn ngoại tiếp của chúng có tâm là giao điểm của hai đường chéo và bán kính bằng một nửa độ dài đường chéo.

7. Đa giác đều

7.1. Đa giác

– Đa giác A₁A₂...A_n (n ≥ 3, n ∈ ℕ) là một hình gồm n đoạn thẳng A₁A₂, A₂A₃, ..., A_{n – 1}A_n, A_nA₁ sao cho mỗi điểm A₁, A₂, ..., A_n là điểm chung của đúng hai đoạn thẳng và không có hai đoạn thẳng nào nằm trên cùng một đường thẳng. Trong đa giác A₁A₂...A_n, các điểm A₁, A₂, ..., A_n là các đỉnh, các đoạn thẳng A₁A₂, A₂A₃, ..., A_{n – 1}A_n, A_nA₁ là các cạnh.

– Nếu với một cạnh bất kì của đa giác, các đỉnh không thuộc cạnh đó đều nằm về một phía đối với đường thẳng chứa cạnh đó thì đa giác được gọi là đa giác lồi.

7.2. Đa giác đều

Định nghĩa: Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.

Chú ý: Các đỉnh của mỗi đa giác đều luôn cùng nằm trên một đường tròn, được gọi là đường tròn ngoại tiếp đa giác, tâm đường tròn được gọi là tâm của đa giác và đa giác được gọi là nội tiếp đường tròn đó.

8. Phép quay

8.1. Khái niệm phép quay

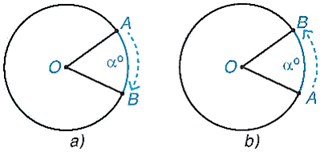
Khái niệm: Phép quay thuận chiều α° (0° < α° < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều quay của kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo α° (Hình a). Định nghĩa tương tự cho phép quay ngược chiều α° tâm O (Hình b).

Chú ý:Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.

8.2. Phép quay giữ nguyên hình đa giác đều

Khái niệm phép quay giữ nguyên hình đa giác đều: Một phép quay được gọi là giữ nguyên một đa giác đều ℋnếu phép quay đó biến mỗi điểm của ℋthành một điểm của ℋ.

Kết quả: Nếu một phép quay biến các đỉnh của đa giác đều ℋthành các đỉnh của ℋthì phép quay đó giữ nguyên ℋ.

Bài tập ôn tập Chương 9

I. Bài tập trắc nghiệm

Bài 1. Khẳng định nào sau đây là sai?

A. Góc nội tiếp của đường tròn là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn;

B. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của cung bị chắn;

C. Trong một đường tròn, các góc nội tiếp chắn các cung bằng nhau thì bằng nhau;

D. Trong một đường tròn, góc nội tiếp chắn cung nhỏ có số đo bằng số đo của góc ở tâm chắn cùng một cung.

Hướng dẫn giải

Đáp án đúng là: D

Phương án A, B, C đúng.

Phương án D sai. Sửa lại: Góc nội tiếp chắn cung nhỏ có số đo bằng nửa số đo của góc ở tâm chắn cùng một cung.

Vậy ta chọn phương án D.

Bài 2. Góc nội tiếp chắn nửa đường tròn là

A. góc vuông;

B. góc nhọn;

C. góc bẹt;

D. góc tù.

Hướng dẫn giải

Đáp án đúng là: A

Góc nội tiếp chắn nửa đường tròn là góc vuông.

Do đó ta chọn phương án A.

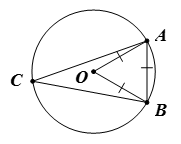
Bài 3. Cho đường tròn (O; R) và dây AB = R. Lấy điểm C thuộc cung lớn AB (C ≠ A, B). Số đo $\widehat{ACB}$ bằng

A. 45°;

B. 30°;

C. 60°;

D. 90°.

Hướng dẫn giải

Đáp án đúng là: B

Ta có OA = OB = AB = R.

Suy ra tam giác OAB đều.Do đó $\widehat{AOB}=60°.$

Xét đường tròn (O), có$\widehat{ACB}$và $\widehat{AOB}$lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ AB nên ta có $\widehat{ACB}=\frac{1}{2}\cdot \widehat{AOB}=\frac{1}{2}\cdot 60°=30°.$

Vậy ta chọn phương án B.

Bài 4. Khẳng định nào sau đây là sai?

A. Trọng tâm của tam giác đều vừa là tâm đường tròn ngoại tiếp, vừa là tâm đường tròn nội tiếp tam giác đều đó;

B. Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác của tam giác đó;

C. Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền;

D. Đường tròn ngoại tiếp một tam giác là đường tròn đi qua nhiều nhất là ba đỉnh của tam giác đó.

Hướng dẫn giải

Đáp án đúng là: D

Phương án A, B, C đúng.

Phương án D sai. Sửa lại: Đường tròn ngoại tiếp một tam giác là đường tròn đi qua cả ba đỉnh của tam giác đó.

Vậy ta chọn phương án D.

Bài 5. Cho tam giác ABC vuông tại A, biết AB = 2 cm và AC = 4 cm. Khi đó bán kính R của đường tròn ngoại tiếp tam giác ABC là

A. $R=2\sqrt{5}$ cm;

B. $R=\sqrt{5}$ cm;

C. R = 10 cm;

D. R = 5 cm.

Hướng dẫn giải

Đáp án đúng là: B

Gọi O là t$AB=4\sqrt{3}$rung điểm của cạnh huyền BC của tam giác ABC vuông tại A.

Khi đó, O là tâm đường tròn ngoại tiếp tam giác ABC.

Xét tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

Suy ra BC² = AB² + AC² = 2² + 4² = 20.

Do đó $BC=2\sqrt{5}$ (cm).

Bán kính đường tròn ngoại tiếp tam giác ABC là: $R=\frac{BC}{2}=\frac{2\sqrt{5}}{2}=\sqrt{5}$ (cm).

Vậy đường tròn ngoại tiếp tam giác ABC có bán kính $R=\sqrt{5}$ cm.

Ta chọn phương án B.

Bài 6. Cho tam giác đều ABC ngoại tiếp đường tròn (O; 4 cm). Khi đó độ dài cạnh AB bằng

A. $AB=\sqrt{3}$ cm;

B. AB = 24 cm;

C. $AB=8\sqrt{3}$ cm;

D. $AB=4\sqrt{3}$ cm.

Hướng dẫn giải

Đáp án đúng là: C

Ta có bán kính đường tròn nội tiếp tam giác đều ABC là: $r=\frac{\sqrt{3}}{6}\cdot AB=4$ (cm).

Suy ra $AB=8\sqrt{3}$ (cm).

Vậy ta chọn phương án C.

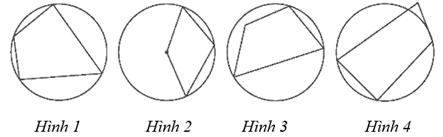
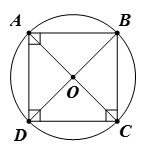
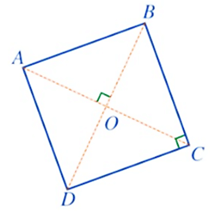
Bài 7. Trong các hình sau, hình nào biểu diễn tứ giác nội tiếp đường tròn?

A. Hình 1;

B. Hình 2;

C. Hình 3;

D. Hình 4.

Hướng dẫn giải

Đáp án đúng là: A

Hình 1 biểu diễn tứ giác nội tiếp đường tròn vì tứ giác có bốn đỉnh nằm trên đường tròn.

Hình 2, 3, 4 không biểu diễn tứ giác nội tiếp đường tròn vì mỗi tứ giác đều có một đỉnh không nằm trên đường tròn.

Vậy ta chọn phương án A.

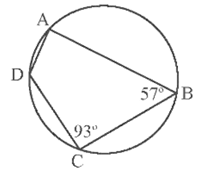
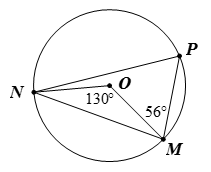
Bài 8. Cho hình vẽ dưới đây.

Khi đó số đo các góc $\widehat{DAB},\widehat{ADC}$ lần lượt bằng

A. 60° và 115°;

B. 90° và 120°;

C. 87° và 123°;

D. 123° và 87°.

Hướng dẫn giải

Đáp án đúng là: C

Ta có tứ giác ABCD nội tiếp đường tròn nên:

⦁ $\widehat{DAB}+\widehat{DCB}=180°$

Do đó $\widehat{DAB}=180°-\widehat{DCB}=180°-93°=87°.$

⦁ $\widehat{ADC}+\widehat{ABC}=180°$

Do đó $\widehat{ADC}=180°-\widehat{ABC}=180°-57°=123°.$

Vậy $\widehat{DAB}=87°;\widehat{ADC}=123°.$

Do đó ta chọn phương án C.

Bài 9. Độ dài cạnh của hình vuông ABCD nội tiếp đường tròn $\left(O;10\sqrt{2}\text{dm}\right)$ là

A. $10\sqrt{2}$ dm;

B. $20\sqrt{2}$ dm;

C. 10 dm;

D. 20 dm.

Hướng dẫn giải

Đáp án đúng là: D

Vì hình vuông ABCD nội tiếp đường tròn $\left(O;10\sqrt{2}\text{dm}\right)$ nên $OB=R=10\sqrt{2}$ (dm).

Suy ra $BD=2OB=2\cdot 10\sqrt{2}=20\sqrt{2}$ (dm).

Vì ABCD là hình vuông nên AB = AD.

Áp dụng định lí Pythagore cho tam giác ABD vuông tại A, ta được:

AB² + AD² = BD².

Suy ra $2A{B}^2={\left(20\sqrt{2}\right)}^2$ hay 2AB² = 800, nên AB² = 400

Do đó AB = 20 (dm) (do AB > 0).

Vậy ta chọn phương án D.

Bài 10. Khẳng định nào sau đây là đúng?

A. Đa giác lồi là đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó;

B. Ngũ giác đều là đa giác có tất cả các cạnh bằng nhau;

C. Ngũ giác đều là đa giác có tất cả các góc bằng nhau;

D. Phép quay giữ nguyên mọi điểm là phép quay 180°.

Hướng dẫn giải

Đáp án đúng là: A

Phương án A đúng.

Phương án B, C sai. Sửa lại: Ngũ giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Phương án D sai. Sửa lại: Phép quay giữ nguyên mọi điểm là phép quay 0° và phép quay 360°.

Vậy ta chọn phương án A.

Bài 11. Cho tam giác đều ABC nội tiếp đường tròn (O). Phép quay giữ nguyên tam giác ABC là

A. Phép quay thuận chiều 270° tâm O;

B. Phép quay thuận chiều 240° tâm O;

C. Phép quay ngược chiều 90° tâm O;

D. Phép quay ngược chiều 140° tâm O.

Hướng dẫn giải

Đáp án đúng là: B

Ba đỉnh A, B, C của tam giác đều ABC chia đường tròn (O) thành ba cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{3}=120°.$

Do đó trong các phương án đã cho, phương án B có phép quay giữ nguyên tam giác ABC là phép quay thuận chiều 240° tâm O.

Vậy ta chọn phương án B.

Bài 12. Có bao nhiêu phép quay biến hình vuông ABCD tâm O thành chính nó?

A. 2;

B. 4;

C. 6;

D. 8.

Hướng dẫn giải

Đáp án đúng là: A

Vì ABCD là hình vuông nên AC ⊥ BD tại O.

Vậy có 8 phép quay biến hình vuông ABCD tâm O thành chính nó là:

– Bốn phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị 90°, 180°, 270°, 360°.

– Bốn phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị 90°, 180°, 270°, 360°.

Do đó ta chọn phương án D.

II. Bài tập tự luận

Bài 1. Xác định số đo các góc của tam giác MNP trong hình vẽ bên dưới.

Hướng dẫn giải

Xét đường tròn (O), có $\widehat{MPN}$ và $\widehat{MON}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ MN nên ta có $\widehat{MPN}=\frac{1}{2}\cdot \widehat{MON}=\frac{1}{2}\cdot 130°=65°.$

Vì OM = ON nên tam giác OMN cân tại O.

Suy ra $\widehat{OMN}=\widehat{ONM}.$

Tam giác OMN, có: $\widehat{MON}+\widehat{OMN}+\widehat{ONM}=180°$ (tổng ba góc của một tam giác)

Suy ra $2\widehat{ONM}=180°-\widehat{MON}=180°-130°=50°.$

Do đó $\widehat{OMN}=\widehat{ONM}=\frac{50°}{2}=25°.$

Vì vậy $\widehat{NMP}=\widehat{OMN}+\widehat{OMP}=25°+56°=81°.$

Tam giác MNP, có: $\widehat{MNP}+\widehat{NMP}+\widehat{MPN}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{MNP}=180°-\left(\widehat{NMP}+\widehat{MPN}\right)=180°-\left(81°+65°\right)=34°.$

Vậy $\widehat{MNP}=180°-\left(\widehat{NMP}+\widehat{MPN}\right)=180°-\left(81°+65°\right)=34°.$

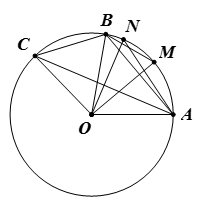
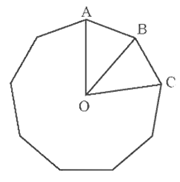
Bài 2. Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho $\widehat{AOB}=80°,\widehat{BOC}=54°,$ điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ AB, AC và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:

a) $\widehat{ACB},\widehat{BAC};$

b) $\widehat{ABM},\widehat{BAN}.$

Hướng dẫn giải

a) Xét đường tròn (O), có $\widehat{ACB}$ và $\widehat{AOB}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ AB nên ta có $\widehat{ACB}=\frac{1}{2}\cdot \widehat{AOB}=\frac{1}{2}\cdot 80°=40°.$

Ta cũng có $\widehat{BAC}$ và $\widehat{BOC}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ BC nên $\widehat{BAC}=\frac{1}{2}\cdot \widehat{BOC}=\frac{1}{2}\cdot 54°=27°.$

Vậy $\widehat{ACB}=40°;\widehat{BAC}=27°.$

b) Điểm M chia cung nhỏ AB thành hai cung bằng nhau nên

$\text{sđ}\stackrel{⏜}{AM}=\text{sđ}\stackrel{⏜}{MB}=\frac{1}{2}\text{sđ}\stackrel{⏜}{AB}=\frac{1}{2}\cdot \widehat{AOB}=40°.$

Ta có $\widehat{ABM}$ là góc nội tiếp chắn cung nhỏ AM trong đường tròn (O) nên

$\widehat{ABM}=\frac{1}{2}\text{sđ}\stackrel{⏜}{AM}=\frac{1}{2}\cdot 40°=20°.$

Ta có $\widehat{AOC}=\widehat{AOB}+\widehat{BOC}=80°+54°=134°.$

Điểm N chia cung nhỏ AC thành hai cung bằng nhau nên

$\text{sđ}\stackrel{⏜}{AN}=\text{sđ}\stackrel{⏜}{NC}=\frac{1}{2}\text{sđ}\stackrel{⏜}{AC}=\frac{1}{2}\cdot \widehat{AOC}=67°.$

Ta thấy $\text{sđ}\stackrel{⏜}{AN}<\text{sđ}\stackrel{⏜}{AB}=\widehat{AOB}$ nên điểm N nằm trên cung nhỏ AB.

Khi đó $\text{sđ}\stackrel{⏜}{NB}=\text{sđ}\stackrel{⏜}{AB}-\text{sđ}\stackrel{⏜}{AN}=\widehat{AOB}-67°=80°-67°=13°.$

Mà$\widehat{BAN}$ là góc nội tiếp chắn cung nhỏ NB nên $\widehat{BAN}=\frac{1}{2}\text{sđ}\stackrel{⏜}{NB}=\frac{1}{2}\cdot 13°=6,5°.$

Vậy $\widehat{ABM}=20°;\widehat{BAN}=6,5°.$

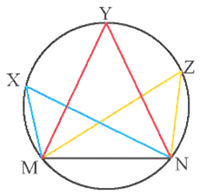
Bài 3. Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (như hình vẽ). Giả sử bóng được đặt ở điểm X thì $\widehat{MXN}$ gọi là góc sút từ vị trí X. Hãy so sánh các góc sút $\widehat{MXN},\widehat{MYN},\widehat{MZN}.$

Hướng dẫn giải

Vì các góc $\widehat{MXN},\widehat{MYN},\widehat{MZN}$ là các góc nội tiếp cùng chắn cung nhỏ MN trong đường tròn nên $\widehat{MXN}=\widehat{MYN}=\widehat{MZN}.$

Vậy các góc sút $\widehat{MXN},\widehat{MYN},\widehat{MZN}$ có số đo bằng nhau.

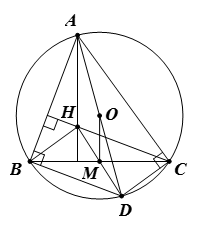
Bài 4. Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O; R) có đường kính AD = 2R. Gọi M là trung điểm BC và H là trực tâm của tam giác ABC. Chứng minh:

a) DB ⊥ AB.

b) Tứ giác BHCD là hình bình hành.

c) AC² + BH² = 4R².

d) Ba điểm H, M, D thẳng hàng.

e) AH = 2OM.

Hướng dẫn giải

a) Ta có $\widehat{ABD}$ là góc nội tiếp chắn nửa đường tròn (O) nên $\widehat{ABD}=90°.$

Vậy DB ⊥ AB.

b) Ta có DB ⊥ AB (câu a) và CH ⊥ AB (do H là trực tâm của tam giác ABC).

Suy ra DB // CH (1)

Chứng minh tương tự câu a, ta có CD ⊥ AC.

Mà BH ⊥ AC (do là trực tâm của tam giác ABC) nên CD // BH (2)

Từ (1), (2), suy ra tứ giác BHCD là hình bình hành.

c) Vì tứ giác BHCD là hình bình hành nên BH = CD.

Áp dụng định lí Pythagore cho ∆ACD vuông tại C, ta được:

AC² + CD² = AD²

Suy ra AC² + BH² = (2R)² = 4R².

Vậy AC² + BH² = 4R².

d) Hình bình hành BHCD có M là trung điểm của đường chéo BC nên M cũng là trung điểm của đường chéo HD.

Vậy ba điểm H, M, D thẳng hàng.

e) Đường tròn (O) có AD là đường kính nên O là trung điểm của AD.

Xét ∆AHD có O, M lần lượt là trung điểm của AD, HD nên OM là đường trung bình của tam giác AHD.

Do đó $OM=\frac{1}{2}AH$ hay AH = 2OM.

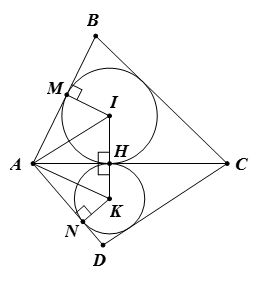
Bài 5. Cho tứ giác ABCD có các tam giác ABC và ADC lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N. Chứng minh:

a) Ba điểm I, H, K thẳng hàng.

b) AM = AN.

c) $\widehat{BAD}=2\widehat{IAK}.$

Hướng dẫn giải

a) Ta có đường tròn (I) tiếp xúc với đường thẳng AC tại điểm H nên AC là tiếp tuyến của đường tròn (I), với H là tiếp điểm hay IH ⊥ AC tại H.

Chứng minh tương tự, ta được KH ⊥ AC tại H.

Vậy ba điểm I, H, K thẳng hàng.

b) Ta có đường tròn (I) tiếp xúc với cạnh AB tại M nên AM là tiếp tuyến của đường tròn (I).

Mà AH cũng là tiếp tuyến của đường tròn (I) và AM, AH cắt nhau tại A, áp dụng tính chất hai tiếp tuyến cắt nhau, ta được AM = AH.

Chứng minh tương tự, ta được AN = AH.

Vậy AM = AN.

c) Ta có AB, AH là các tiếp tuyến của đường tròn (I) cắt nhau tại A, áp dụng tính chất hai tiếp tuyến cắt nhau, ta được $\widehat{BAI}=\widehat{IAH}.$

Chứng minh tương tự, ta được $\widehat{DAK}=\widehat{KAH}.$

Ta có $\widehat{BAD}=\widehat{BAI}+\widehat{IAH}+\widehat{HAK}+\widehat{KAD}$

 $=2\widehat{IAH}+2\widehat{KAH}=2\left(\widehat{IAH}+\widehat{KAH}\right)=2\widehat{IAK}.$

Vậy $\widehat{BAD}=2\widehat{IAK}.$

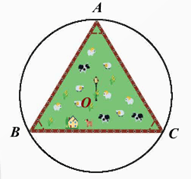
Bài 6. Một trang trại nuôi gia súc có dạng hình tam giác đều cạnh 150 m (như hình vẽ). Người ta muốn đặt một trụ đèn cao áp tại một điểm cách đều ba đỉnh của tam giác đều. Nêu cách xác định vị trí đặt đèn và tính khoảng cách từ điểm đó đến ba đỉnh của tam giác (làm tròn kết quả đến hàng phần mười).

Hướng dẫn giải

Gọi O là vị trí cần đặt đèn. Gọi A, B, C là ba đỉnh của tam giác đều (như hình vẽ).

Vì O cách đều ba đỉnh A, B, C của tam giác đều ABC nên O là tâm đường tròn ngoại tiếp tam giác ABC.

Suy ra khoảng cách từ vị trí O đến mỗi vị trí A, B, C là bán kính của đường tròn ngoại tiếp tam giác đều ABC.

Do đó $OA=OB=OC=\frac{\sqrt{3}}{3}\cdot 150=50\sqrt{3}\approx 86,6$ (m).

Vậy khoảng cách từ vị trí đặt đèn O đến ba đỉnh của tam giác đều ABC bằng khoảng 86,6 m.

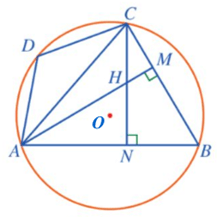
Bài 7. Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho tam giác ABC nhọn. Hai đường cao AM, CN của tam giác ABC cắt nhau tại H. Chứng minh:

a) $\widehat{MHN}+\widehat{ABC}=180°.$

b) $\widehat{AHC}=\widehat{ADC}.$

c) $\widehat{ADC}=\widehat{BAM}+90°.$

Hướng dẫn giải

a) Ta có $\widehat{HMB}=\widehat{HNB}=90°$ (do AM, CN là hai đường cao cắt nhau tại H của tam giác ABC).

Do đó hai điểm M, N cùng nằm trên đường tròn đường kính HB.

Khi đó tứ giác HMBN nội tiếp đường tròn đường kính HB.

Vậy $\widehat{MHN}+\widehat{MBN}=180°$ hay $\widehat{MHN}+\widehat{ABC}=180°.$

b) Ta có tứ giác ABCD nội tiếp đường tròn (O) nên $\widehat{ADC}+\widehat{ABC}=180°.$

Mà $\widehat{MHN}+\widehat{ABC}=180°$ (câu a) nên $\widehat{ADC}=\widehat{MHN}.$

Lại có $\widehat{AHC}=\widehat{MHN}$(cặp góc đối đỉnh) nên $\widehat{AHC}=\widehat{ADC}.$

c) Tam giác ABM, có: $\widehat{AMB}+\widehat{BAM}+\widehat{ABC}=180°$ (tổng ba góc của một tam giác)

Mà $\widehat{ADC}+\widehat{ABC}=180°$ (chứng minh trên)

Suy ra $\widehat{ADC}=\widehat{AMB}+\widehat{BAM}=90°+\widehat{BAM}.$

Vậy $\widehat{ADC}=\widehat{BAM}+90°.$

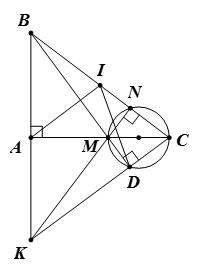
Bài 8. Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên đoạn AC, đường tròn đường kính CM cắt hai đường thẳng BM và BC lần lượt tại D và N. Chứng minh rằng:

a) Tứ giác ABCD nội tiếp.

b) Các đường thẳng AB, MN, CD cùng đi qua một điểm.

Hướng dẫn giải

a) Gọi I là trung điểm BC. Khi đó, $IB=IC=\frac{1}{2}BC.$

Ta có $\widehat{CDM}=90°$ (góc nội tiếp chắn nửa đường tròn đường kính CM).

Suy ra tam giác BCD vuông tại D.

Do đó $ID=\frac{1}{2}BC$ (tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông). Suy ra IB = IC = ID.

Tương tự đối với ∆ABC vuông tại A, ta cũng có IA = IB = IC.

Do đó, IA = IB = IC = ID.

Vậy tứ giác ABCD nội tiếp đường tròn tâm I, đường kính BC.

b) Ta có $\widehat{MNC}=90°$ (góc nội tiếp chắn nửa đường tròn đường kính CM).

Suy ra MN ⊥ BC.

Xét ∆BMC có: MN ⊥ BC, CD ⊥ BM và AB ⊥ MC nên AB, MN, CD là ba đường cao của tam giác, do đó ba đường cao AB, MN, CD cắt nhau tại trực tâm K của tam giác BMC.

Vậy các đường thẳng AB, MN, CD cùng đi qua một điểm.

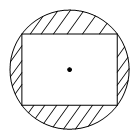
Bài 9. Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 6 cm và 4 cm (như hình vẽ).

Tính diện tích phần bị gạch chéo (làm tròn kết quả đến hàng phần trăm).

Hướng dẫn giải

Áp dụng định lí Pythagore, ta có độ dài đường chéo của hình chữ nhật là:

$\sqrt{6^2+4^2}=\sqrt{52}=2\sqrt{13}$ (cm).

Hình chữ nhật nội tiếp đường tròn nên đường kính của đường tròn chính là độ dài của đường chéo hình chữ nhật.

Bán kính đường tròn là: $R=\frac{2\sqrt{13}}{2}=\sqrt{13}$ (cm).

Diện tích hình chữ nhật là: S_hcn = 6.4 = 24 (cm²).

Diện tích hình tròn là: S_{hình tròn} = πR² = 13π (cm²).

Diện tích phần bị gạch chéo là: S = S_tròn – S_hcn = 13π – 24 ≈ 16,84 (cm²).

Vậy diện tích phần bị gạch chéo bằng khoảng 16,84 cm².

Bài 10. Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Đa giác MNPQRS có phải là đa giác đều không? Vì sao?

Hướng dẫn giải

Gọi O là tâm của lục giác đều ABCDEF.

Sáu đỉnh A, B, C, D, E, F của lục giác đều ABCDEF chia đường tròn (O) thành sáu cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{6}=60°.$

Suy ra $\widehat{AOB}=\text{sđ}\stackrel{⏜}{AB}=60°.$

Mà ∆AOB cân tại O (do OA = OB).Do đó ∆AOB đều.

Vì vậy $\widehat{OAB}=\widehat{OBA}=\widehat{AOB}=60°.$

Chứng minh tương tự, ta được $\widehat{OBC}=60°.$

Khi đó ta có $\widehat{ABC}=\widehat{OBA}+\widehat{OBC}=60°+60°=120°.$

Chứng minh tương tự, ta được $\widehat{BCD}=\widehat{CDE}=\widehat{DEF}=\widehat{EFA}=\widehat{FAB}=\widehat{ABC}=120°.$

Ta có ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA.

Mà M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA.

Suy ra AM = MB = BN = NC = CP = PD = DQ = QE = ER = RF = FS = SA.

Xét ∆SAM và ∆MBN, có:

$\widehat{SAM}=\widehat{MBN};$

AM = BN (chứng minh trên);

SA = MB (chứng minh trên).

Do đó ∆SAM = ∆MBN (c.g.c)

Suy ra SM = MN (cặp cạnh tương ứng).

Chứng minh tương tự, ta được MN = NP, NP = PQ, PQ = QR, QR = RS.

Do đó MN = NP = PQ = QR = RS = SM (1)

Vì SA = AM (chứng minh trên) nên tam giác SAM cân tại A.

Suy ra $\widehat{ASM}=\widehat{AMS}.$

Tam giác SAM, có: $\widehat{SAM}+\widehat{ASM}+\widehat{AMS}=180°$ (tổng ba góc của một tam giác)

Suy ra $2\widehat{AMS}=180°-\widehat{SAM}=180°-120°=60°.$

Khi đó $\widehat{ASM}=\widehat{AMS}=\frac{60°}{2}=30°.$

Tương tự như vậy, ta thu được: $\widehat{BMN}=\widehat{BNM}=30°.$

Ta có $\widehat{AMS}+\widehat{SMN}+\widehat{BMN}=180°$ (kề bù)

Suy ra $\widehat{SMN}=180°-\left(\widehat{AMS}+\widehat{BMN}\right)=180°-\left(30°+30°\right)=120°.$

Chứng minh tương tự, ta được:

$\widehat{MNP}=\widehat{NPQ}=\widehat{PQR}=\widehat{QRS}=\widehat{RSM}=\widehat{SMN}=120°$ (2)

Từ (1), (2), ta suy ra đa giác MNPQRS là đa giác đều.

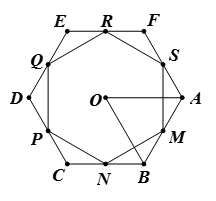
Bài 11. Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh của đa giác (như hình vẽ).

a) Tìm số đo các góc $\widehat{AOB},\widehat{ABO},\widehat{ABC}.$

b) Tìm phép quay thuận chiều tâm O biến điểm A thành điểm C.

c) Tìm các phép quay biến đa giác đã cho thành chính nó.

Hướng dẫn giải

a) Đa giác đều đã cho có 9 cạnh nên đa giác đều này có 9 đỉnh.

Chín đỉnh của đa giác đều đã cho chia đường tròn (O) thành chín cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{9}=40°.$

Tức là, $\widehat{AOB}=\widehat{BOC}=40°.$

Vì OA = OB nên tam giác AOB cân tại O.

Suy ra $\widehat{OAB}=\widehat{ABO}.$

Tam giác AOB, có: $\widehat{AOB}+\widehat{OAB}+\widehat{ABO}=180°$ (tổng ba góc của một tam giác)

Suy ra $2\widehat{ABO}=180°-\widehat{AOB}=180°-40°=140°.$

Do đó $\widehat{OAB}=\widehat{ABO}=\frac{140°}{2}=70°.$

Thực hiện tương tự, ta được $\widehat{OBC}=\widehat{OCB}=70°.$

Ta có $\widehat{ABC}=\widehat{ABO}+\widehat{OBC}=70°+70°=140°.$

Vậy $\widehat{AOB}=40°;\widehat{ABO}=70°;\widehat{ABC}=140°.$

b) Ta có: $\widehat{AOC}=\widehat{AOB}+\widehat{BOC}=40°+40°=80°.$

Mà OA = OC nên tia OA quay thuận chiều 80° tâm O đến tia OC.

Vậy phép quay thuận chiều 80° tâm O biến điểm A thành điểm C.

c) Có 18 phép quay biến đa giác đã cho thành chính nó là:

– Chín phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị 40°, 80°, 120°, 160°, 200°, 240°, 280°, 320°, 360°.

– Chín phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị 40°, 80°, 120°, 160°, 200°, 240°, 280°, 320°, 360°.

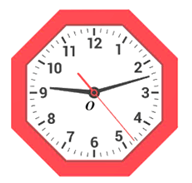
Bài 12. Đường viền ngoài của chiếc đồng hồ trong hình vẽ bên được làm theo hình đa giác đều nào? Tìm phép quay giữ nguyên đa giác đều đó.

Hướng dẫn giải

Đường viền ngoài của chiếc đồng hồ trong hình vẽ được làm theo hình bát giác đều (vì có 8 cạnh).

Tám đỉnh của bát giác đều chia đường tròn (O) thành tám cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{8}=45°.$

Có 16 phép quay giữ nguyên đa giác đều đó là:

– Tám phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360°.

– Tám phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360°.

Học tốt Toán 9 Chương 9

Các bài học để học tốt Bài tập cuối chương 9 Toán lớp 9 hay khác:

• Giải sgk Toán 9: Bài tập cuối chương 9