Lý thuyết Toán lớp 9 Đa giác đều - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 9 Bài 30: Đa giác đều sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán lớp 9 Đa giác đều - Kết nối tri thức

Lý thuyết Đa giác đều

1. Đa giác đều

1.1. Đa giác

Đa giác A₁A₂...A_n (n ≥ 3, n ∈ ℕ) là một hình gồm n đoạn thẳng A₁A₂, A₂A₃, ..., A_{n – 1}A_n, A_nA₁ sao cho mỗi điểm A₁, A₂, ..., A_n là điểm chung của đúng hai đoạn thẳng và không có hai đoạn thẳng nào nằm trên cùng một đường thẳng. Trong đa giác A₁A₂...A_n, các điểm A₁, A₂, ..., A_n là các đỉnh, các đoạn thẳng A₁A₂, A₂A₃, ..., A_{n – 1}A_n, A_nA₁ là các cạnh.

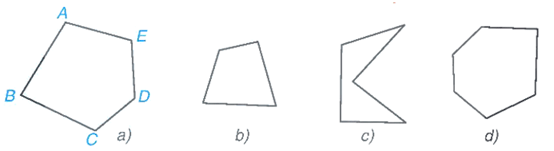
Chẳng hạn, những hình như hình dưới đây được gọi chung là các đa giác.

⦁ Đa giác ABCDE (Hình a) là hình gồm năm đoạn thẳng AB, BC, CD, DE, EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng. Đa giác ABCDE có năm đỉnh là các điểm A, B, C, D, E; năm cạnh là các đoạn thẳng AB, BC, CD, DE, EA và năm góc là các góc EAB, ABC, BCD, CDE, DEA.

⦁ Nếu với một cạnh bất kì của đa giác, các đỉnh không thuộc cạnh đó đều nằm về một phía đối với đường thẳng chứa cạnh đó thì đa giác được gọi là đa giác lồi. Các đa giác trong Hình a, b, d là các đa giác lồi. Đa giác trong Hình c không phải đa giác lồi.

1.2. Đa giác đều

Định nghĩa: Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.

Chú ý: Các đỉnh của mỗi đa giác đều luôn cùng nằm trên một đường tròn, được gọi là đường tròn ngoại tiếp đa giác, tâm đường tròn được gọi là tâm của đa giác và đa giác được gọi là nội tiếp đường tròn đó.

Ví dụ 1. Dưới đây là hình các đa giác đều thường gặp trong hình học:

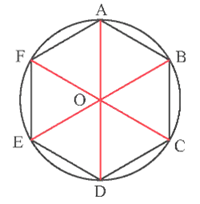
Ví dụ 2. Cho đường tròn (O; R). Lấy các điểm A, B, C, D, E, F trên đường tròn (O; R) sao cho số đo các cung $\stackrel{⏜}{AB},\stackrel{⏜}{BC},\stackrel{⏜}{CD},\stackrel{⏜}{DE},\stackrel{⏜}{EF},\stackrel{⏜}{FA}$ bằng nhau. Đa giác ABCDEF có phải là đa giác đều không? Vì sao?

Hướng dẫn giải

Ta có các cung $\stackrel{⏜}{AB},\stackrel{⏜}{BC},\stackrel{⏜}{CD},\stackrel{⏜}{DE},\stackrel{⏜}{EF},\stackrel{⏜}{FA}$ chia đường tròn (O; R) thành sáu cung bằng nhau.

Suy ra mỗi cung có số đo bằng $\frac{360°}{6}=60°.$

Ta có $\widehat{AOB}$ là góc ở tâm chắn cung nhỏ AB.

Suy ra $\widehat{AOB}=\text{sđ}\stackrel{⏜}{AB}=60°.$

Tam giác AOB, có: OA = OB = R và $\widehat{AOB}=60°$ nên tam giác AOB đều.

Do đó AB = OA = R và $\widehat{ABO}=60°$ (1)

Chứng minh tương tự, ta được BC = OB = R và $\widehat{OBC}=60°$ (2)

Từ (1), (2), ta suy ra AB = BC = R và $\widehat{ABC}=\widehat{ABO}+\widehat{OBC}=60°+60°=120°.$

Chứng minh tương tự, ta thu được đa giác ABCDEF có các cạnh đều bằng R và các góc đều bằng 120°.

Vậy đa giác ABCDEF là một đa giác đều.

2. Phép quay

2.1. Khái niệm phép quay

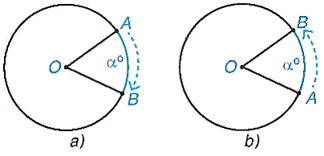
Khái niệm: Phép quay thuận chiều α° (0° < α° < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều quay của kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo α° (Hình a). Định nghĩa tương tự cho phép quay ngược chiều α° tâm O (Hình b).

Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.

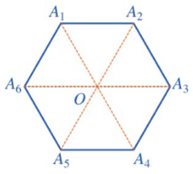
Ví dụ 3. Cho hình lục giác đều A₁A₂A₃A₄A₅A₆ có tâm O. Chỉ ra phép quay tâm O sao cho phép quay đó biến mỗi điểm A₁, A₂, A₃, A₄, A₅, A₆ thành điểm đối xứng với nó qua tâm O.

Hướng dẫn giải

Do A₁A₂A₃A₄A₅A_6­ là hình lục giác đều nên ba đường chéo A₁A₄, A₂A₅, A₃A₆ cắt nhau tại trung điểm O của mỗi đường.

Điểm đối xứng của mỗi điểm A₁, A₂, A₃, A₄, A₅, A₆ theo thứ tự là A₄, A₅, A₆, A₁, A₂, A₃.

Vậy các phép quay tâm O biến mỗi điểm A₁, A₂, A₃, A₄, A₅, A₆ thành điểm đối xứng với nó qua tâm O là:

– Phép quay thuận chiều 180° tâm O;

– Phép quay ngược chiều 180° tâm O.

2.2. Phép quay giữ nguyên hình đa giác đều

Khái niệm phép quay giữ nguyên hình đa giác đều: Một phép quay được gọi là giữ nguyên một đa giác đều ℋ nếu phép quay đó biến mỗi điểm của ℋ thành một điểm của ℋ.

Kết quả: Nếu một phép quay biến các đỉnh của đa giác đều ℋ thành các đỉnh của ℋ thì phép quay đó giữ nguyên ℋ.

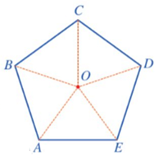
Ví dụ 4. Cho ngũ giác đều ABCDE tâm O (như hình vẽ).

a) Phép quay thuận chiều tâm O biến điểm A thành điểm B thì các điểm B, C, D, E tương ứng biến thành các điểm nào?

b) Chỉ ra các phép quay tâm O giữ nguyên ngũ giác đều ABCDE.

Hướng dẫn giải

a) Năm đỉnh A, B, C, D, E của ngũ giác đều ABCDE chia đường tròn (O) thành năm cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{5}=72°.$

Suy ra phép quay thuận chiều 72° tâm O biến điểm A thành điểm B.

Vậy phép quay thuận chiều 72° tâm O biến các điểm B, C, D, E theo thứ tự thành các điểm C, D, E, A.

b) Có 10 phép quay giữ nguyên ngũ giác đều ABCDE là:

– Năm phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị 72°, 144°, 216°, 288°, 360°.

– Năm phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị 72°, 144°, 216°, 288°, 360°.

Bài tập Đa giác đều

Bài 1. Khẳng định nào sau đây là đúng?

A. Đa giác lồi là đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó;

B. Ngũ giác đều là đa giác có tất cả các cạnh bằng nhau;

C. Ngũ giác đều là đa giác có tất cả các góc bằng nhau;

D. Phép quay giữ nguyên mọi điểm là phép quay 180°.

Hướng dẫn giải

Đáp án đúng là: A

Phương án A đúng.

Phương án B, C sai. Sửa lại: Ngũ giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Phương án D sai. Sửa lại: Phép quay giữ nguyên mọi điểm là phép quay 0° và phép quay 360°.

Vậy ta chọn phương án A.

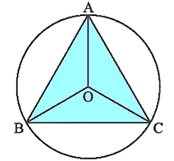
Bài 2. Cho tam giác đều ABC nội tiếp đường tròn (O). Phép quay giữ nguyên tam giác ABC là

A. Phép quay thuận chiều 270° tâm O;

B. Phép quay thuận chiều 240° tâm O;

C. Phép quay ngược chiều 90° tâm O;

D. Phép quay ngược chiều 140° tâm O.

Hướng dẫn giải

Đáp án đúng là: B

Ba đỉnh A, B, C của tam giác đều ABC chia đường tròn (O) thành ba cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{3}=120°.$

Do đó trong các phương án đã cho, phương án B có phép quay giữ nguyên tam giác ABC là phép quay thuận chiều 240° tâm O.

Vậy ta chọn phương án B.

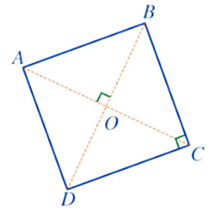
Bài 3. Có bao nhiêu phép quay biến hình vuông ABCD tâm O thành chính nó?

A. 2;

B. 4;

C. 6;

D. 8.

Hướng dẫn giải

Đáp án đúng là: A

Vì ABCD là hình vuông nên AC ⊥ BD tại O.

Vậy có 8 phép quay biến hình vuông ABCD tâm O thành chính nó là:

– Bốn phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị 90°, 180°, 270°, 360°.

– Bốn phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị 90°, 180°, 270°, 360°.

Do đó ta chọn phương án D.

Bài 4. Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Đa giác MNPQRS có phải là đa giác đều không? Vì sao?

Hướng dẫn giải

Gọi O là tâm của lục giác đều ABCDEF.

Sáu đỉnh A, B, C, D, E, F của lục giác đều ABCDEF chia đường tròn (O) thành sáu cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{6}=60°.$

Suy ra $\widehat{AOB}=\text{sđ}\stackrel{⏜}{AB}=60°.$

Mà ∆AOB cân tại O (do OA = OB).Do đó ∆AOB đều.

Vì vậy $\widehat{OAB}=\widehat{OBA}=\widehat{AOB}=60°.$

Chứng minh tương tự, ta được $\widehat{OBC}=60°.$

Khi đó ta có $\widehat{ABC}=\widehat{OBA}+\widehat{OBC}=60°+60°=120°.$

Chứng minh tương tự, ta được $\widehat{BCD}=\widehat{CDE}=\widehat{DEF}=\widehat{EFA}=\widehat{FAB}=\widehat{ABC}=120°.$

Ta có ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA.

Mà M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA.

Suy ra AM = MB = BN = NC = CP = PD = DQ = QE = ER = RF = FS = SA.

Xét ∆SAM và ∆MBN, có:

$\widehat{SAM}=\widehat{MBN};$

AM = BN (chứng minh trên);

SA = MB (chứng minh trên).

Do đó ∆SAM = ∆MBN (c.g.c)

Suy ra SM = MN (cặp cạnh tương ứng).

Chứng minh tương tự, ta được MN = NP, NP = PQ, PQ = QR, QR = RS.

Do đó MN = NP = PQ = QR = RS = SM (1)

Vì SA = AM (chứng minh trên) nên tam giác SAM cân tại A.

Suy ra $\widehat{ASM}=\widehat{AMS}.$

Tam giác SAM, có: $\widehat{SAM}+\widehat{ASM}+\widehat{AMS}=180°$ (tổng ba góc của một tam giác)

Suy ra $2\widehat{AMS}=180°-\widehat{SAM}=180°-120°=60°.$

Khi đó $\widehat{ASM}=\widehat{AMS}=\frac{60°}{2}=30°.$

Tương tự như vậy, ta thu được: $\widehat{BMN}=\widehat{BNM}=30°.$

Ta có $\widehat{AMS}+\widehat{SMN}+\widehat{BMN}=180°$ (kề bù)

Suy ra $\widehat{SMN}=180°-\left(\widehat{AMS}+\widehat{BMN}\right)=180°-\left(30°+30°\right)=120°.$

Chứng minh tương tự, ta được:

$\widehat{MNP}=\widehat{NPQ}=\widehat{PQR}=\widehat{QRS}=\widehat{RSM}=\widehat{SMN}=120°$ (2)

Từ (1), (2), ta suy ra đa giác MNPQRS là đa giác đều.

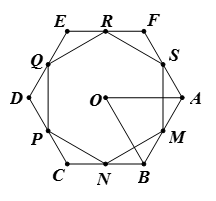
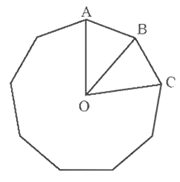
Bài 5. Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh của đa giác (như hình vẽ).

a) Tìm số đo các góc $\widehat{AOB},\widehat{ABO},\widehat{ABC}.$

b) Tìm phép quay thuận chiều tâm O biến điểm A thành điểm C.

c) Tìm các phép quay biến đa giác đã cho thành chính nó.

Hướng dẫn giải

a) Đa giác đều đã cho có 9 cạnh nên đa giác đều này có 9 đỉnh.

Chín đỉnh của đa giác đều đã cho chia đường tròn (O) thành chín cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{9}=40°.$

Tức là, $\widehat{AOB}=\widehat{BOC}=40°.$

Vì OA = OB nên tam giác AOB cân tại O.

Suy ra $\widehat{OAB}=\widehat{ABO}.$

Tam giác AOB, có: $\widehat{AOB}+\widehat{OAB}+\widehat{ABO}=180°$ (tổng ba góc của một tam giác)

Suy ra $2\widehat{ABO}=180°-\widehat{AOB}=180°-40°=140°.$

Do đó $\widehat{OAB}=\widehat{ABO}=\frac{140°}{2}=70°.$

Thực hiện tương tự, ta được $\widehat{OBC}=\widehat{OCB}=70°.$

Ta có $\widehat{ABC}=\widehat{ABO}+\widehat{OBC}=70°+70°=140°.$

Vậy $\widehat{AOB}=40°;\widehat{ABO}=70°;\widehat{ABC}=140°.$

b) Ta có: $\widehat{AOC}=\widehat{AOB}+\widehat{BOC}=40°+40°=80°.$

Mà OA = OC nên tia OA quay thuận chiều 80° tâm O đến tia OC.

Vậy phép quay thuận chiều 80° tâm O biến điểm A thành điểm C.

c) Có 18 phép quay biến đa giác đã cho thành chính nó là:

– Chín phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị 40°, 80°, 120°, 160°, 200°, 240°, 280°, 320°, 360°.

– Chín phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị 40°, 80°, 120°, 160°, 200°, 240°, 280°, 320°, 360°.

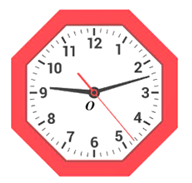
Bài 6. Đường viền ngoài của chiếc đồng hồ trong hình vẽ bên được làm theo hình đa giác đều nào? Tìm phép quay giữ nguyên đa giác đều đó.

Hướng dẫn giải

Đường viền ngoài của chiếc đồng hồ trong hình vẽ được làm theo hình bát giác đều (vì có 8 cạnh).

Tám đỉnh của bát giác đều chia đường tròn (O) thành tám cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{8}=45°.$

Có 16 phép quay giữ nguyên đa giác đều đó là:

– Tám phép quay thuận chiều α° tâm O với α° lần lượt nhận các giá trị 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360°.

– Tám phép quay ngược chiều α° tâm O với α° lần lượt nhận các giá trị 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360°.

Học tốt Đa giác đều

Các bài học để học tốt Đa giác đều Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài 30: Đa giác đều