Giải Toán 9 trang 77 Tập 1 Kết nối tri thức

---

Với Giải Toán 9 trang 77 Tập 1 trong Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng Toán 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 dễ dàng làm bài tập Toán 9 trang 77.

Giải Toán 9 trang 77 Tập 1 Kết nối tri thức

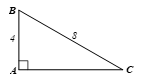
Luyện tập 3 trang 77 Toán 9 Tập 1: Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến chữ số thập phân thứ ba) và các góc B, C (làm tròn đến độ).

Lời giải:

Xét ∆ABC vuông tại A.

Cách 1: Theo định lí Pythagore, ta có:

$AC=\sqrt{B{C}^2-A{B}^2}=\sqrt{8^2-4^2}=\sqrt{48}\approx \mathrm{6,928.}$

Ta có $\cos B=\frac{AB}{BC}=\frac{4}{8}=\frac{1}{2}.$

Từ đó tìm được $\widehat{B}=60°,$ suy ra $\widehat{C}=90°-\widehat{B}=90°-60°=30°.$

Cách 2: Ta có $\cos B=\frac{AB}{BC}=\frac{4}{8}=\frac{1}{2}.$

Từ đó tìm được $\widehat{B}=60°,$ suy ra $\widehat{C}=90°-\widehat{B}=90°-60°=30°.$

Ta có $\sin B=\frac{AC}{BC},$ suy ra $\sin 60°=\frac{AC}{8},$ do đó AC = 8.sin60° ≈ 6,928.

Câu hỏi trang 77 Toán 9 Tập 1:

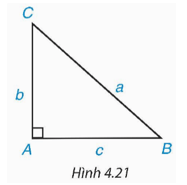
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b hoặc AB = c, BC = a và không sử dụng định lí Pythagore (H.4.21).

2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.

Lời giải:

1. Trường hợp biết AB = c và AC = b, ta cần tính BC và các góc của tam giác.

Xét ∆ABC vuông tại A, sử dụng định nghĩa tỉ số lượng giác tan, ta có: $\tan B=\frac{AC}{AB}=\frac{b}{c}.$ Từ đó ta tính được góc B, khi đó ta tính được góc C thông qua định lí tổng ba góc của một tam giác.

Sau đó, sử dụng định lí 1, ta có AC = BC.sinB, suy ra $BC=\frac{AC}{\sin B}=\frac{b}{\sin B}.$

Trường hợp biết AB = c và BC = a, ta cần tính AC và các góc của tam giác.

Xét ∆ABC vuông tại A, sử dụng định nghĩa tỉ số lượng giác cos, ta có: $\cos B=\frac{AB}{BC}=\frac{c}{a}.$ Từ đó ta tính được góc B, khi đó ta tính được góc C thông qua định lí tổng ba góc của một tam giác.

Sau đó, sử dụng định lí 1, ta có AC = BC.sinB = a.sinB.

2.

Trường hợp biết cạnh góc vuông AB và góc B, ta cần tính số đo góc C và các cạnh AC, BC:

Ta tính được góc C thông qua định lí tổng ba góc của một tam giác.

Xét ∆ABC vuông tại A, sử dụng định lí 1, ta có: AB = BC.cosB, suy ra $BC=\frac{AB}{\cos B}.$

Sử dụng định lí 2, ta có AC = AB.tanB.

Trường hợp biết biết cạnh huyền BC và góc B, ta cần tính số đo góc C và các cạnh AB, AC:

Ta tính được góc C thông qua định lí tổng ba góc của một tam giác.

Xét ∆ABC vuông tại A, sử dụng định lí 1, ta có: AB = BC.cosB và AC = BC.sinB.

Lưu ý: Ngoài cách giải đã nêu, ta cũng có nhiều cách giải khác cho bài toán.

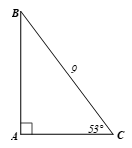
Luyện tập 4 trang 77 Toán 9 Tập 1: Giải tam giác ABC vuông tại A, biết BC = 9, $\widehat{C}=53°.$

Lời giải:

Xét ∆ABC vuông tại A, ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$(định lí tổng ba góc của một tam giác).

Suy ra $\widehat{B}=90°-\widehat{C}=90°-53°=37°.$

Theo định lí 1, ta có:

⦁ AC = BC.cosC = 9.cos53° ≈ 5,416.

⦁ AB = BC.sinC = 9.sin53° ≈ 7,188.

Vậy ∆ABC có $\widehat{A}=90°,\widehat{B}=37°,\widehat{C}=53°,AB\approx \mathrm{7,188,}AC\approx \mathrm{5,416,}BC=9.$

Vận dụng trang 77 Toán 9 Tập 1: Giải bài toán ở tình huống mở đầu với α = 27° và β = 19°.

Lời giải:

Xét ∆M’P’H vuông tại H, theo định lí 2, ta có: M’H = P’H.cotα.

Xét ∆N’P’H vuông tại H, theo định lí 2, ta có: N’H = P’H.cotβ.

Mà N’H = N’M’ + M’H = MN + M’H

Do đó P’H.cotβ = MN + P’H.cotα.

Suy ra P’H.(cotβ – cotα) = MN nên $P^{\text{'}}H=\frac{MN}{cot\beta –cot\alpha }=\frac{20}{cot\beta –cot\alpha }.$

Vì vậy, $P^{\text{'}}P=P^{\text{'}}H+HP=\frac{20}{cot\beta –cot\alpha }+\mathrm{1,6}$

$=\frac{20}{\cot 19°-\cot 27°}\text{+1,6}\approx \text{22,84 (m)}$

Vậy chiều cao của tòa nhà là khoảng 22,84 (m).

Lời giải bài tập Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng hay khác:

• Giải Toán 9 trang 74
• Giải Toán 9 trang 75
• Giải Toán 9 trang 78