Giải Toán 9 trang 78 Tập 1 Kết nối tri thức

---

Với Giải Toán 9 trang 78 Tập 1 trong Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng Toán 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 dễ dàng làm bài tập Toán 9 trang 78.

Giải Toán 9 trang 78 Tập 1 Kết nối tri thức

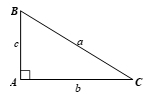
Bài 4.8 trang 78 Toán 9 Tập 1: Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:

a) a = 21, b = 18;

b) b = 10, $\widehat{C}=30°;$

c) c = 5, b = 3.

Lời giải:

a) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có: a² = b² + c²

Suy ra $c=\sqrt{a^2-b^2}=\sqrt{{21}^2-{18}^2}=\sqrt{117}=\sqrt{3^2\cdot 13}=3\sqrt{13}$ (do c > 0).

Theo định nghĩa tỉ số lượng giác sin, ta có $\sin B=\frac{b}{a}=\frac{18}{21}=\frac{6}{7}.$Từ đó tìm được $\widehat{B}\approx 59°.$

Theo định lí tổng ba góc của một tam giác, ta có $\widehat{A}+\widehat{B}+\widehat{C}=180°.$

Suy ra $\widehat{C}=90°-\widehat{B}\approx 90°-59°=31°.$

Vậy ∆ABC có $\widehat{A}=90°,\widehat{B}\approx 59°,\widehat{C}\approx 31°,a=\mathrm{21,}b=\mathrm{18,}c=3\sqrt{13}.$

b) Xét ∆ABC vuông tại A, theo định lí tổng ba góc của một tam giác, ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180°.$

Suy ra $\widehat{B}=90°-\widehat{C}=90°-30°=60°.$

Theo định lí 2, ta có: $AB=c=b\cdot tanC=10\cdot tan30°=\frac{10\sqrt{3}}{3}.$

Theo định lí 1, ta có AC = b = a.cosC, suy ra $a=\frac{b}{\cos C}=\frac{10}{\cos 30°}=\frac{10}{\frac{\sqrt{3}}{2}}=\frac{20}{\sqrt{3}}=\frac{20\sqrt{3}}{3}.$

Vậy ∆ABC có $\widehat{A}=90°,\widehat{B}=60°,\widehat{C}=30°,a=\frac{20\sqrt{3}}{3},b=\mathrm{10,}c=\frac{10\sqrt{3}}{3}.$

c) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có: a² = b² + c²

Suy ra $a=\sqrt{b^2+c^2}=\sqrt{3^2+5^2}=\sqrt{34}$ (vì a > 0).

Theo định nghĩa tỉ số lượng giác tan, ta có $\tan B=\frac{b}{c}=\frac{3}{5},$ suy ra $\widehat{B}\approx 31°.$

Theo định lí tổng ba góc của một tam giác, ta có $\widehat{A}+\widehat{B}+\widehat{C}=180°.$

Suy ra $\widehat{C}=90°-\widehat{B}\approx 90°-31°=59°.$

Vậy ∆ABC có $\widehat{A}=90°,\widehat{B}\approx 31°,\widehat{C}\approx 59°,a=\sqrt{34},b=\mathrm{3,}c=5.$

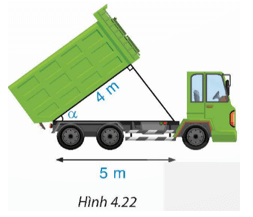
Bài 4.9 trang 78 Toán 9 Tập 1: Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22.

Lời giải:

Theo định nghĩa tỉ số lượng giác cos, ta có $\cos \alpha =\frac{4}{5},$ từ đó tính được α ≈ 36°52’.

Vậy góc nghiêng α của thùng xe chở rác khoảng 36°52’.

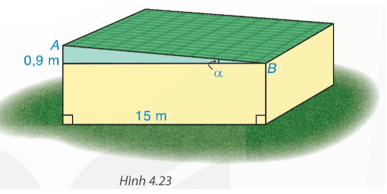
Bài 4.10 trang 78 Toán 9 Tập 1: Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.

Lời giải:

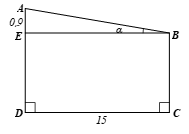
Theo đề ta có hình vẽ:

Tứ giác BCDE là hình chữ nhật nên BE = CD = 15 m.

Xét ∆ABE vuông tại E, theo định nghĩa tỉ số lượng giác tan, ta có:

$\tan B=\frac{AE}{BE}=\frac{\mathrm{0,9}}{15}=\mathrm{0,06.}$ Từ đó tìm được $\widehat{B}\approx 3°{26}^{\text{'}}.$

Theo định lí Pythagore, ta có: AB² = AE² + BE².

Suy ra $AB=\sqrt{A{E}^2+B{E}^2}=\sqrt{{\mathrm{0,9}}^2+{15}^2}\approx \mathrm{15,027}\text{ (m)}$ (do AB > 0).

Vậy góc nghiêng của mái nhà kho khoảng 3°26’ và chiều rộng của mái nhà kho khoảng 15,027 m.

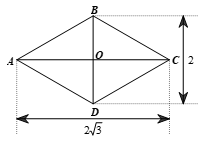
Bài 4.11 trang 78 Toán 9 Tập 1: Tính các góc của hình thoi có hai đường chéo dài $2\sqrt{3}$ và 2.

Lời giải:

Theo đề ta có hình vẽ:

Hình thoi ABCD có hai đường chéo lần lượt là $AC=2\sqrt{3};$ BD = 2 và AC cắt BD tại O. Khi đó AC ⊥ BD; O là trung điểm của AC, BD.

Suy ra $OA=\frac{AC}{2}=\frac{2\sqrt{3}}{2}=\sqrt{3}$ và $OB=\frac{BD}{2}=\frac{2}{2}=1.$

Xét ∆OAB vuông tại O, theo định nghĩa tỉ số lượng giác tan, ta có:

$\tan \widehat{BAO}=\frac{OB}{OA}=\frac{1}{\sqrt{3}},$ suy ra $\widehat{BAO}=30°.$

Theo định lí tổng ba góc của một tam giác, ta có $\widehat{AOB}+\widehat{BAO}+\widehat{ABO}=180°.$

Suy ra $\widehat{ABO}=90°-\widehat{BAO}=90°-30°=60°.$

Hình thoi ABCD có AC, BD là đường chéo nên AC, BD lần lượt là tia phân giác của $\widehat{BAD},\widehat{ABC}.$

Mà $\widehat{A}=\widehat{C};\widehat{B}=\widehat{D}$ (tính chất hình thoi) nên $\widehat{A}=\widehat{C}=2\widehat{BAO}=2\cdot 30°=60°$ và $\widehat{B}=\widehat{D}=2\widehat{ABO}=2\cdot 60°=120°.$

Vậy $\widehat{A}=\widehat{C}=60°$ và $\widehat{B}=\widehat{D}=120°.$

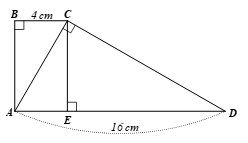
Bài 4.12 trang 78 Toán 9 Tập 1: Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm và $\widehat{A}=\widehat{B}=\widehat{ACD}=90°.$

a) Kẻ đường cao CE của tam giác ACD. Chứng minh $\widehat{ADC}=\widehat{ACE}.$ Tính sin của các góc $\widehat{ADC},\widehat{ACE}$ và suy ra AC² = AE.AD. Từ đó tính AC.

b) Tính góc D của hình thang.

Lời giải:

a) Ta có $\widehat{ADC}+\widehat{DCE}=90°$ (hai góc nhọn trong ∆CDE vuông tại E) và $\widehat{ACE}+\widehat{DCE}=\widehat{ACD}=90°$ nên $\widehat{ADC}=\widehat{ACE}$ (cùng phụ góc $\widehat{DCE}).$(1)

Xét ∆ACD vuông tại C, ta có $\sin \widehat{ADC}=\frac{AC}{AD}.$(2)

Xét ∆ACE vuông tại E, ta có $\sin \widehat{ACE}=\frac{AE}{AC}.$(3)

Từ (1), (2) và (3) ta suy ra $\frac{AC}{AD}=\frac{AE}{AC},$ do đó AC² = AE.AD.

Hình thang ABCD có AD // BC và AB ⊥ BC (do $\widehat{B}=90°)$ nên AB ⊥ AD.

Tứ giác ABCE có $\widehat{A}=\widehat{B}=\widehat{E}=90°$ nên ABCE là hình chữ nhật.

Suy ra AE = BC = 4 cm (tính chất hình chữ nhật).

Khi đó, AC² = 4.16 = 64 nên AC = 8 (cm) (do AC > 0).

b) Theo câu a, ta có $\sin \widehat{ADC}=\frac{AC}{AD}=\frac{8}{16}=\frac{1}{2},$ suy ra $\widehat{D}=30°.$

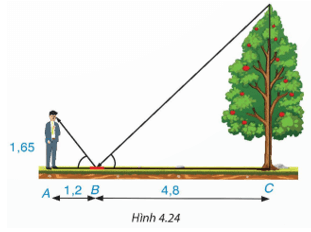
Bài 4.13 trang 78 Toán 9 Tập 1: Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).

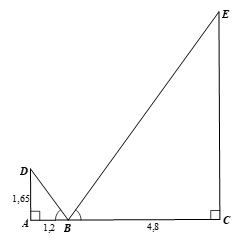
Lời giải:

Theo đề ta có hình vẽ:

Xét ∆ABD vuông tại A, ta có $\tan \widehat{ABD}=\frac{AD}{AB}=\frac{\mathrm{1,65}}{\mathrm{1,2}}=\frac{11}{8}.$

Mà $\widehat{ABD}=\widehat{CBE}$ nên $\tan \widehat{CBE}=\frac{11}{8}.$

Xét ∆BCE vuông tại C, ta có $CE=BC\cdot tan\widehat{CBE}=\mathrm{4,8}\cdot \frac{11}{8}=\mathrm{6,6}$(m).

Vậy chiều cao của cây là 6,6 m.

Lời giải bài tập Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng hay khác:

• Giải Toán 9 trang 74
• Giải Toán 9 trang 75
• Giải Toán 9 trang 77