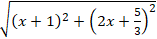Các bài toán cực trị liên quan đến đường thẳng - Toán lớp 10
Các bài toán cực trị liên quan đến đường thẳng
Với Các bài toán cực trị liên quan đến đường thẳng Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập cực trị liên quan đến đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 10.
A. Phương pháp giải
Để giải các bài toán cực trị liên quan tới đường thẳng ta sử dụng các phương pháp:
+ Sử dụng bất đẳng thức tam giác; bất đẳng thức Cosi.
+ Biểu thức : A2 + b ≥ b và -A2 + b ≤ b
+ Tính chất y = ax2 + bx + c
- Nếu a > 0 hàm số đạt giá trị nhỏ nhất tại x =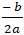 
- Nếu a < 0 thì hàm số đạt giá trị lớn nhất tại x =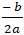
B. Ví dụ minh họa
Ví dụ 1: Tồn tại điểm M(x;y) trên đường thẳng d: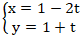 
sao cho x2 + y2 nhỏ nhất.
Tính 2x - y?
A. – 1 B. 0 C. 1 D. 2
Lời giải
+ Điểm M thuộc d nên tọa độ M(1 - 2t; 1 + t).
⇒ x2 + y2 = (1 - 2t)2 + (1 + t)2 = 1 - 4t + 4t2 + 1 + 2t + t2
= 5t2 - 2t + 2
+ Biểu thức f(t) = 5t2 - 2t + 2 đạt giá trị nhỏ nhất khi và chỉ khi t =
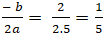
Vậy x2 + y2 đạt giá trị nhỏ nhất là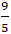 
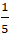
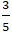
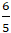
khi t = 
. Khi đó tọa độ điểm M( 
; 
)
⇒ 2x - y = 0
Chọn B.
Ví dụ 2: Tìm trên trục hoành điểm P sao cho tổng khoảng cách từ P đến các điểm
A( 1; 1) và B( 2; - 4) nhỏ nhất?
A. P(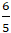
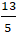
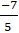
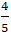
; 0)
B. P( 
; 0)
C. P( 
; 0)
D. P( 
; 0)
Lời giải
+ Nhận xét: A và B nằm khác phía so với Ox.
+ Phương trình AB: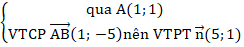 
⇒ Phương trình AB: 5(x - 1) + 1(y - 1) = 0 hay 5x + y - 6 = 0.
+ Gọi H là giao điểm của AB và trục Ox. Tọa độ H là nghiệm hệ:
⇒ H(
; 0)
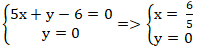
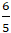
+ Với ba điểm A; P và B bất kì ta có: PA + PB ≥ AB
⇒ (PA + PB)min khi và chỉ khi 3 điểm A; P và B thẳng hàng
⇒ P ≡ H
Chọn A.
Ví dụ 3: Tìm trên trục hoành điểm P sao cho tổng khoảng cách từ P đến A(1 ; 1) và
B(3 ; 3) là nhỏ nhất?
A. P(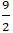 
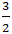
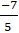
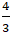
; 0)
B. P( 
; 0)
C. P(
; 0)
D. P( 
; 0)
Lời giải
+ Nhận xét : Hai điểm A và B nằm cùng phía so với trục Ox.
+ Gọi A1 đối xứng với A qua trục Ox. Suy ra A1 (1; -1)
+ Phương trình A1B: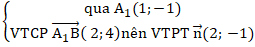 
⇒ Phương trình A1B: 2(x - 1) – 1(y + 1) = 0 hay 2x - y - 3 = 0.
+ Gọi H là giao điểm của A1B và Ox nên tọa độ H là nghiệm hệ:
⇒ H(
; 0)
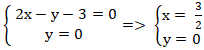
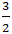
+ ta có: PA + PB = PA1 + PB ≥ AB
⇒ PA + PBmin ⇔ A1; P; B thẳng hàng
⇔ P ≡ H.
Chọn B.
Ví dụ 4: Cho điểm M( 4; 1). Một đường thẳng d đi qua M cắt Ox; Oy theo thứ tự tại
A( a; 0)
và B( 0; b) với a;b > 0. Viết phương trình đường thẳng d sao cho diện tích tam giác OAB nhỏ nhất?
A. 5x + 4y + 8 = 0 B. 2x + 3y - 8 = 0 C. x + 4y - 8 = 0 D. x + 4y + 8 = 0
Lời giải
+ Đường thẳng d qua A(a;0) và B(0;b).
⇒ Phương trình đoạn chắn AB: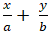 
= 1
Vì M thuộc d nên :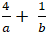 
= 1 (1)
+ ta có diện tích tam giác OAB là:
S = 
OA.OB =
ab (vì tam giác OAB vuông tại O).
+ Từ (1) suy ra: 1 =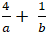
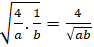
≥ 2.
( Bất đẳng thức Cosi)
⇔ ab ≥ 16 nên S ≥ 8
⇒ Smin = 8.
Dấu “=” đặt được khi: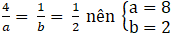 
Khi đó phương trình đường thẳng (d) là x + 4y - 8 = 0
Chọn C.
Ví dụ 5: Cho điểm M( 4; 1). Một đường thẳng d đi qua M cắt Ox; Oy theo thứ tự tại
A( a; 0) và
B( 0; b) với a;b > 0. Viết phương trình đường thẳng d sao cho OA + OB nhỏ nhất?
A. x + 2y - 6 = 0 B. 2x + 3y - 8 = 0 C. x + 4y - 8 = 0 D. x + 4y +8 = 0
Lời giải
+ Đường thẳng d qua A( a; 0) và B( 0; b).
⇒ Phương trình đoạn chắn AB: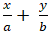
= 1
Vì M thuộc d nên :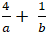
= 1 (1)
+ Từ (1) suy ra: a =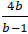 
⇒ điều kiện b > 1.
Khi đó: OA + OB = a + b=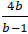
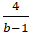
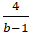
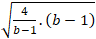
+ b = 
+ b + 4
=
+ b - 1 + 5 ≥ 2.
+ 5 = 9 ( bất đẳng thức cosi)
⇒ (OA+ OB)min = 9. Dấu “=” đạt được khi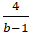
= b - 1 = 2 nên a = 6 và b = 3
Khi đó phương trình đường thẳng d: x + 2y - 6 = 0.
Chọn A.
Ví dụ 6: Cho điểm M( 4; 1). Một đường thẳng d đi qua M cắt Ox; Oy theo thứ tự tại
A(a ; 0) và B( 0; b) với a; b > 0. Viết phương trình đường thẳng d sao cho
nhỏ nhất?
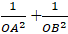
A. 5x + 2y - 6 = 0 B. 2x + 3y - 8 = 0 C. x + 4y - 8 = 0 D. 4x + 2y - 17 = 0
Lời giải
+ Đường thẳng d qua A( a; 0) và B( 0; b).
⇒ Phương trình đoạn chắn AB: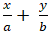
= 1
Vì M thuộc d nên :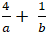
= 1 (1)
+ Áp dụng bất đẳng thức bunhia scopki (ax + by)2 ≤ (a2 + b2).(x2 + y2).
⇒ 1 = (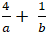
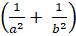
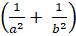
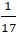
)2 ≤ (42 + 12).
⇒
≥ 
Vậy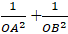
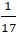
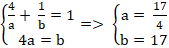
nhỏ nhất là
; đạt được khi: 
Khi đó phương trình đường thẳng d là: 4x + 2y - 17 = 0
Chọn D.
Ví dụ 7: Cho điểm M(3; -2) và đường thẳng (d): 2x - y = 0. Tìm điểm A trên d sao khoảng cách AM là ngắn nhất?
A. A(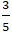
; -
).
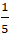
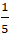
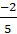
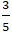
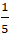
B. A( -
; 
).
C. A(
;
).
D. Tất cả sai
Lời giải
+ Điểm A thuộc d nên A( t; 2t) .
+ Để khoảng cách AM ngắn nhất thì A là hình chiếu vuông góc của M lên đường thẳng d.
⇒ Đường thẳng d vuông góc với đường thẳng AM.
+ Đường thẳng AM: 
⇒ Phương trình AM: 1(x - 3) + 2( y + 2) = 0 hay x + 2y + 1 = 0
+ Đường thẳng AM và d cắt nhau tại A nên tọa độ A là nghiệm hệ:
⇒ A( -
;
).
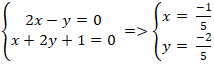
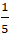
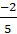
Chọn B.
C. Bài tập vận dụng
Câu 1: Tìm trên đường thẳng d: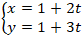 
điểm M( x; y) sao cho x2 + y2 đạt giá trị nhỏ nhất?
A. M(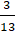 
; - 
)
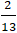
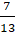
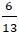
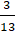
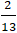
B. M( 
; - 
)
C. M(
;
)
D. Đáp án khác
Lời giải:
Đáp án: A
Trả lời:
+ Điểm M(1 + 2t; 1 + 3t) thuộc d.
⇒ x2 + y2 = (1 + 2t)2 + (1 + 3t)2
= 1 + 4t + 4t2 + 1 + 6t + 9t2 = 13t2 + 10t + 2.
+ Biểu thức f(t) = 13t2 + 10t + 2 đạt giá trị nhỏ nhất tại t =
= 
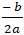
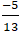
⇒( x2 + y2)min =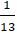 
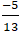
đạt được khi t =
⇒ Tọa độ điểm M(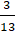
; -
)
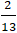
Câu 2: Tìm trên trục hoành điểm P sao cho tổng khoảng cách từ P đến các điểm A(2;3) và B(1; -2) nhỏ nhất?
A. P(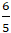
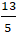
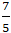
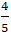
; 0)
B. P(
; 0)
C. P( 
; 0)
D. P(
; 0)
Lời giải:
Đáp án: C
Trả lời:
+ Nhận xét: A và B nằm khác phía so với Ox.
+ Phương trình AB: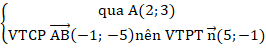 
⇒ Phương trình AB: 5(x - 2) - 1(y - 3) = 0 hay 5x – y - 7 = 0.
+ Gọi H là giao điểm của AB và trục Ox. Tọa độ H là nghiệm hệ:
⇒ H(
; 0)
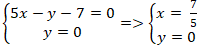
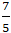
+ Với ba điểm A; P và B bất kì ta có: PA + PB ≥ AB
⇒ (PA + PB)min khi và chỉ khi 3 điểm A; P và B thẳng hàng
⇒ P ≡ H
Câu 3: Tìm trên trục hoành điểm P sao cho tổng khoảng cách từ P đến A(3; 1) và B(1; 4) là nhỏ nhất?
A. P(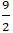
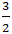
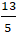
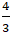
; 0)
B. P(
; 0)
C. P(
; 0)
D. P(
; 0)
Lời giải:
Đáp án: C
Trả lời:
+ Nhận xét : Hai điểm A và B nằm cùng phía so với trục Ox.
+ Gọi A1 đối xứng với A qua trục Ox. Suy ra A1 (3; -1)
+ Phương trình A1B: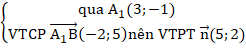 
⇒ Phương trình A1B: 5(x - 3) + 2(y + 1) = 0 hay 5x + 2y - 13 = 0.
+ Gọi H là giao điểm của A1B và Ox nên tọa độ H là nghiệm hệ:
⇒ H(
; 0)
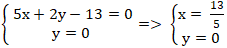
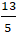
+ ta có: PA + PB = PA1 + PB ≥ AB
⇒ PA + PBmin ⇔ A1; P; B thẳng hàng
⇔ P ≡ H.
Câu 4: Cho điểm M(1; 16). Một đường thẳng d đi qua M cắt Ox; Oy theo thứ tự tại
A(a; 0) và
B(0; b) với a;b > 0. Viết phương trình đường thẳng d sao cho diện tích tam giác OAB nhỏ nhất?
A.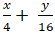 
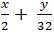
= 1
B. 2x + 3y - 8 = 0
C. 
= 1
D. x + 4y + 8 = 0
Lời giải:
Đáp án: C
Trả lời:
+ Đường thẳng d qua A(a; 0) và B(0; b).
⇒ Phương trình đoạn chắn AB: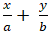
= 1
Vì M thuộc d nên :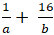 
= 1 (1)
+ ta có diện tích tam giác OAB là:
S =
OA.OB =
ab (vì tam giác OAB vuông tại O).
+ Từ (1) suy ra: 1 =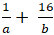
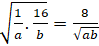
≥ 2.
( Bất đẳng thức Cosi)
⇔ ab ≥ 64 nên S ≥ 32
⇒ Smin = 32.
Dấu “=” đặt được khi: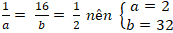 
Khi đó phương trình đường thẳng (d) là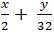
= 1
Câu 5: Cho điểm M(16;1). Một đường thẳng d đi qua M cắt Ox; Oy theo thứ tự tại
A(a; 0) và B(0; b)
với a;b > 0. Viết phương trình đường thẳng d sao cho OA + OB nhỏ nhất?
A. x + 4y - 20 = 0 B. 2x + 3y - 8 = 0 C. x + 4y - 8 = 0 D. x + 4y +8 = 0
Lời giải:
Đáp án: A
Trả lời:
+ Đường thẳng d qua A(a; 0) và B(0; b).
⇒ Phương trình đoạn chắn AB: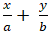
= 1
Vì M thuộc d nên :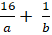 
= 1 (1)
+ Từ (1) suy ra: a =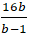 
⇒ điều kiện b > 1.
Khi đó: OA + OB = a + b =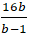
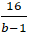
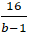
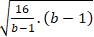
+ b = 
+ b + 16
=
+ b - 1 + 17 ≥ 2.
+ 17 = 25 ( bất đẳng thức cosi)
⇒ (OA + OB)min = 25. Dấu “=” đạt được khi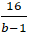
= b - 1 nên a = 20 và b = 5
Khi đó phương trình đường thẳng d: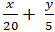 
= 1 hay x + 4y - 20 = 0
Câu 6: Cho điểm M( 1; 1). Một đường thẳng d đi qua M cắt Ox; Oy theo thứ tự tại
A(a; 0) và B(0; b)
với a;b > 0. Viết phương trình đường thẳng d sao cho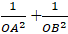
nhỏ nhất?
A. 5x + 2y - 6 = 0 B. 2x + 3y - 8 = 0 C. x + 4y - 8 = 0 D. x + y - 2 = 0
Lời giải:
Đáp án: D
Trả lời:
+ Đường thẳng d qua A(a; 0) và B(0; b).
⇒ Phương trình đoạn chắn AB: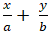
= 1
Vì M thuộc d nên :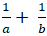 
= 1 (1)
+ Áp dụng bất đẳng thức bunhia scopki (ax + by)2 ≤ (a2 + b2).(x2 + y2).
⇒ 1 = (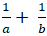
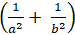
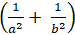
)2 ≤ (12 + 12).
⇒
≥
Vậy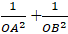
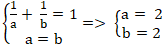
nhỏ nhất là
; đạt được khi: 
Khi đó; phương trình đường thẳng d là: x + y - 2 = 0
Câu 7: Cho điểm M(2; -1) và đường thẳng (d): x + 2y - 3 = 0. Tìm điểm A trên d sao khoảng cách AM là ngắn nhất?
A. A(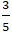
; -
).
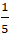
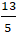
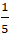
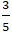
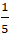
B. A(
;
).
C. A(
;
).
D. Tất cả sai
Lời giải:
Đáp án: B
Trả lời:
+ Điểm A thuộc d nên A(3 - 2t; t) .
+ Để khoảng cách AM ngắn nhất thì A là hình chiếu vuông góc của M lên đường thẳng d.
⇒ Đường thẳng d vuông góc với đường thẳng AM.
+ Đường thẳng AM: 
⇒ Phương trình AM: 2(x - 2) - 1(y + 1) = 0 hay 2x - y - 5 = 0.
+ Đường thẳng AM và d cắt nhau tại A nên tọa độ A là nghiệm hệ:
⇒ A(
;
).
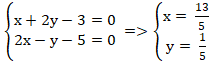
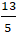
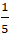
Câu 8: Cho ba điểm A( -6 ; 3) ; B(0 ; -1) và C( 3 ; 2). Điểm M trên đường thẳng
d: 2x - y + 3 = 0
mà | MA→ + MB→ + MC→| nhỏ nhất là:
A. M(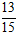
; 
)
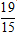
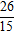
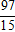
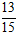
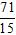
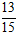
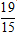
B. M(
; 
)
C. M(
; 
)
D. M( -
;
)
Lời giải:
Đáp án: D
Trả lời:
M(x; y) ∈ D => M(x; 2x + 3). Suy ra: MA→ = ( - x - 6; - 2x), MB→ = ( - x; - 2x - 4),
MC→ = ( - x + 3; - 2x - 1).
Do đó: MA→ + MB→ + MC→ = ( -3x - 3; -6x - 5)
| MA→ + MB→ + MC→| =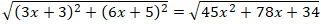 
| MA→ + MB→ + MC→| nhỏ nhất ⇔ f(x) = 45x2 + 78x + 34 nhỏ nhất ⇔
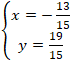
Ghi chú. Giải cách khác: MA→ + MB→ + MC→ = 3MG→ nên:
| MA→ + MB→ + MC→| nhỏ nhất ⇔ MG→ nhỏ nhất.
Mà G(-1;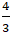
), M(x; 2x + 3) nên ta có:
|MG→| = MG = 
nhỏ nhất ⇒ x = -
⇒ y =
⇒ M( -
;
)
